题目内容
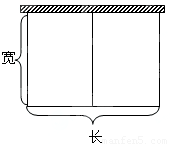 如图,以墙为一边用篱笆围成长方形的场地,并用平行于一边的篱笆隔开.已知篱笆总长为80米.
如图,以墙为一边用篱笆围成长方形的场地,并用平行于一边的篱笆隔开.已知篱笆总长为80米.(Ⅰ)把场地面积S(米2)表示为场地宽x(米)的函数,并指出函数的定义域.
(Ⅱ)这块场地的长和宽各为多少时,场地面积最大,最大面积是多少?
【答案】分析:(I)由题意设长方形场地的宽为x,则长为80-3x,表示出面积y,根据长宽均为正,可得函数的定义域
(II)对(I)中所得进行配方求出函数的最值即场地的面积最大值,从而求解.
解答:解:(I)设长方形场地的宽为x,则长为80-3x,
它的面积y=x(80-3x)=-3x2+80x
由长方形的长和宽均为正,故0<x<
即函数的定义域为:(0, )
)
(II)由y=x(80-3x)=-3(x- )2+
)2+ .
.
当宽x= 时,这块长方形场地的面积最大,
时,这块长方形场地的面积最大,
这时的长为80-3x=80-3× =40,
=40,
最大面积为 米2.
米2.
点评:此题是一道实际应用题,考查函数的最值问题,解决此类问题要运用配方法,这也是高考常考的方法.
(II)对(I)中所得进行配方求出函数的最值即场地的面积最大值,从而求解.
解答:解:(I)设长方形场地的宽为x,则长为80-3x,
它的面积y=x(80-3x)=-3x2+80x
由长方形的长和宽均为正,故0<x<

即函数的定义域为:(0,
 )
)(II)由y=x(80-3x)=-3(x-
 )2+
)2+ .
.当宽x=
 时,这块长方形场地的面积最大,
时,这块长方形场地的面积最大,这时的长为80-3x=80-3×
 =40,
=40,最大面积为
 米2.
米2.点评:此题是一道实际应用题,考查函数的最值问题,解决此类问题要运用配方法,这也是高考常考的方法.

练习册系列答案
相关题目
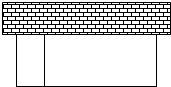
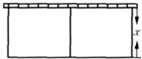 如图,以墙为一边用篱笆围成长方形的场地,并用平行于一边的篱笆隔开.已知篱笆总长为60米.
如图,以墙为一边用篱笆围成长方形的场地,并用平行于一边的篱笆隔开.已知篱笆总长为60米.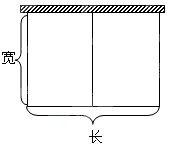 如图,以墙为一边用篱笆围成长方形的场地,并用平行于一边的篱笆隔开.已知篱笆总长为80米.
如图,以墙为一边用篱笆围成长方形的场地,并用平行于一边的篱笆隔开.已知篱笆总长为80米.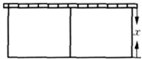 如图,以墙为一边用篱笆围成长方形的场地,并用平行于一边的篱笆隔开.已知篱笆总长为60米.
如图,以墙为一边用篱笆围成长方形的场地,并用平行于一边的篱笆隔开.已知篱笆总长为60米.