题目内容
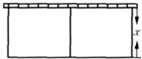 如图,以墙为一边用篱笆围成长方形的场地,并用平行于一边的篱笆隔开.已知篱笆总长为60米.
如图,以墙为一边用篱笆围成长方形的场地,并用平行于一边的篱笆隔开.已知篱笆总长为60米.(Ⅰ)把场地面积S(米2)表示为场地宽x(米)的函数,并指出函数的定义域;
(Ⅱ)这块场地的长和宽各为多少时,场地面积最大?最大面积是多少?
分析:(Ⅰ)由篱笆总长为60米得场地长为(60-3x)米,由矩形面积公式可得S,由
可得函数定义域;
(Ⅱ)根据二次函数的性质可求面积的最大值及相应x值;
|
(Ⅱ)根据二次函数的性质可求面积的最大值及相应x值;
解答:解:(Ⅰ)由于篱笆总长为60米,所以场地长为(60-3x)米,
故S=x(60-3x)=-3x2+60x,
由于
,可得0<x<20,即函数的定义域为(0,20);
(Ⅱ)由S=-3x2+60x=-3(x-10)2+300,
当x=10时,Smax=300(米2),
故当场地的长和宽分别为30米和10米时,场地有最大面积300平方米.
故S=x(60-3x)=-3x2+60x,
由于
|
(Ⅱ)由S=-3x2+60x=-3(x-10)2+300,
当x=10时,Smax=300(米2),
故当场地的长和宽分别为30米和10米时,场地有最大面积300平方米.
点评:本题考查函数在解决实际问题中的应用,属中档题,求定义域时要考虑实际意义.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
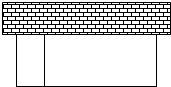
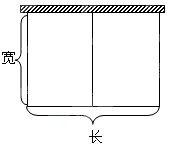 如图,以墙为一边用篱笆围成长方形的场地,并用平行于一边的篱笆隔开.已知篱笆总长为80米.
如图,以墙为一边用篱笆围成长方形的场地,并用平行于一边的篱笆隔开.已知篱笆总长为80米.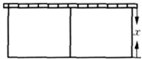 如图,以墙为一边用篱笆围成长方形的场地,并用平行于一边的篱笆隔开.已知篱笆总长为60米.
如图,以墙为一边用篱笆围成长方形的场地,并用平行于一边的篱笆隔开.已知篱笆总长为60米.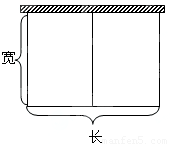 如图,以墙为一边用篱笆围成长方形的场地,并用平行于一边的篱笆隔开.已知篱笆总长为80米.
如图,以墙为一边用篱笆围成长方形的场地,并用平行于一边的篱笆隔开.已知篱笆总长为80米.