题目内容
((本题满分14分)
已知 与
与 都是边长为2的等边三角形,且平面
都是边长为2的等边三角形,且平面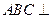 平面
平面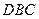 ,过点
,过点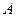 作
作 平面
平面 ,且
,且 .
.

(Ⅰ)求证: 平面
平面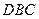 ;
;
(Ⅱ)求直线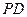 与平面
与平面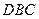 所成角的大小.
所成角的大小.
已知
 与
与 都是边长为2的等边三角形,且平面
都是边长为2的等边三角形,且平面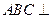 平面
平面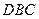 ,过点
,过点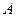 作
作 平面
平面 ,且
,且 .
.
(Ⅰ)求证:
 平面
平面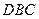 ;
;(Ⅱ)求直线
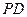 与平面
与平面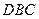 所成角的大小.
所成角的大小.解:(Ⅰ)取 的中点
的中点 ,连接
,连接 ,则
,则 . …………(1分)
. …………(1分)
又∵平面 平面
平面 ,平面
,平面 平面
平面
 ,
,
∴ 平面
平面 . ……………………………………(3分)
. ……………………………………(3分)
而 平面
平面 ,∴
,∴ . ……………………(4分)
. ……………………(4分)
又∵ 在平面
在平面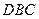 内,
内, ∴
∴ 平面
平面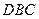 . …(7分)
. …(7分)
(Ⅱ)∵ ,∴
,∴ 四点共线.连接
四点共线.连接 并延长交
并延长交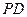 延长线为
延长线为 .
.

∵平面 平面
平面 ,平面
,平面 平面
平面
 ,
,
 ,
,
∴ 平面
平面 ,∴直线
,∴直线 即直线
即直线 在
在
平面 内的射影.
内的射影.
∴ 即直线
即直线 平面
平面
所成的角. ………………(10分)
∵ ,∴
,∴ 的中位线.∴
的中位线.∴ .
.
又∵ ,∴
,∴
∴ …………………………(13分)
…………………………(13分)
因此直线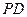 与平面
与平面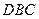 所成角为
所成角为 ………………………(14分)
………………………(14分)
 的中点
的中点 ,连接
,连接 ,则
,则 . …………(1分)
. …………(1分)又∵平面
 平面
平面 ,平面
,平面 平面
平面
 ,
,∴
 平面
平面 . ……………………………………(3分)
. ……………………………………(3分)而
 平面
平面 ,∴
,∴ . ……………………(4分)
. ……………………(4分)又∵
 在平面
在平面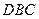 内,
内, ∴
∴ 平面
平面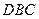 . …(7分)
. …(7分)(Ⅱ)∵
 ,∴
,∴ 四点共线.连接
四点共线.连接 并延长交
并延长交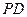 延长线为
延长线为 .
.
∵平面
 平面
平面 ,平面
,平面 平面
平面
 ,
, ,
,∴
 平面
平面 ,∴直线
,∴直线 即直线
即直线 在
在平面
 内的射影.
内的射影.∴
 即直线
即直线 平面
平面
所成的角. ………………(10分)
∵
 ,∴
,∴ 的中位线.∴
的中位线.∴ .
. 又∵
 ,∴
,∴
∴
 …………………………(13分)
…………………………(13分)因此直线
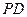 与平面
与平面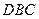 所成角为
所成角为 ………………………(14分)
………………………(14分)略

练习册系列答案
相关题目
 中,
中, 是等腰直角三角形,
是等腰直角三角形, ,
, 和
和 都垂直于平面
都垂直于平面 ,且
,且 ,点
,点 是
是 的中点。
的中点。
 平面
平面 与面
与面 .
.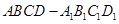 中,底面为正方形,侧棱垂直于底面,
中,底面为正方形,侧棱垂直于底面,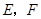 分别是
分别是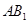 ,
,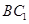 的中点,则以下结论中不成立的为( ).
的中点,则以下结论中不成立的为( ).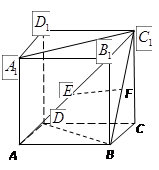
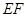 与
与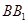 垂直
垂直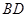 垂直
垂直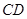 异面
异面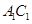 异面
异面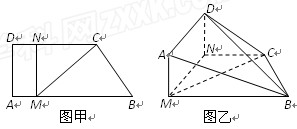
 ?
?
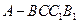 中,
中,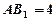 .底面
.底面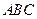 是正三角形,
是正三角形,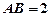 .四边形
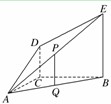
.四边形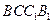 是矩形,二面角
是矩形,二面角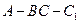 为直二面角.
为直二面角.
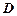 在
在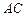 上运动,当
上运动,当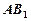 ∥平面
∥平面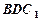 ,
, 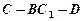 余弦值.
余弦值. 的底面是正六边形,
的底面是正六边形, 平面
平面 .则下列结论不正确的是
.则下列结论不正确的是
 平面
平面

 平面
平面 平面
平面

