题目内容
设点A,B是椭圆C:x2+4y2=8上的两点,且|AB|=2,点F为椭圆C的右焦点,O为坐标原点.
(Ⅰ)若
•
=0,且点A在第一象限,求点A的坐标;
(Ⅱ)求△AOB面积的最小值.
(Ⅰ)若
| OF |
| AB |
(Ⅱ)求△AOB面积的最小值.
分析:(Ⅰ)由
•
=0,知
⊥
,可判断点A、B关于x轴对称,由|AB|=2可得点A纵坐标,代入椭圆方程可得其横坐标;
(Ⅱ)设直线AB的方程为:y=mx+n,由
,得(1+4m2)x2+8mnx+4n2-8=0,利用韦达定理即弦长公式可得m,n的方程①,由点到直线的距离公式可得点P到直线AB的距离d,代入①消掉n可得d关于m的表达式,由此可得其最小值,则△AOB面积S=d,可得其最小值;
| OF |
| AB |
| OF |
| AB |
(Ⅱ)设直线AB的方程为:y=mx+n,由
|
解答:解:(Ⅰ)由
•
=0,知
⊥
,
又|AB|=2,点A在第一象限,
所以点A、B关于x轴对称,可设A(x,1)(x>0),
代入椭圆方程得,x2+4=8,解得x=2,
所以点A的坐标为(2,1);
(Ⅱ)设直线AB的方程为:y=mx+n,
由
,得(1+4m2)x2+8mnx+4n2-8=0,
△=64m2n2-4(1+4m2)(4n2-8)>0,即8m2-n2+2>0,
设A(x1,y1),B(x2,y2),
则x1+x2=-
,x1x2=
,
由|AB|=2,则
|x1-x2|=2,即(1+m2)[(x1+x2)2-4x1x2]=4,
则(1+m2)[
-4•
]=4,化简得,
16m4+32m2-4n2-4m2n2+7=0①,
点P到直线AB的距离d=
,则n2=d2(1+m2),
代入①,并整理可得4d2=
=16-
≥16-9=7,当m=0时取等号,
所以d≥
,
所以△AOB面积S=
|AB|•d=d≥
,即所求面积的最小值为
.
| OF |
| AB |
| OF |
| AB |
又|AB|=2,点A在第一象限,
所以点A、B关于x轴对称,可设A(x,1)(x>0),
代入椭圆方程得,x2+4=8,解得x=2,
所以点A的坐标为(2,1);
(Ⅱ)设直线AB的方程为:y=mx+n,
由
|
△=64m2n2-4(1+4m2)(4n2-8)>0,即8m2-n2+2>0,
设A(x1,y1),B(x2,y2),
则x1+x2=-
| 8mn |
| 1+4m2 |
| 4n2-8 |
| 1+4m2 |
由|AB|=2,则
| 1+m2 |
则(1+m2)[
| 64m2n2 |
| (1+4m2)2 |
| 4n2-8 |
| 1+4m2 |
16m4+32m2-4n2-4m2n2+7=0①,
点P到直线AB的距离d=
| |n| | ||
|
代入①,并整理可得4d2=
| 16m4+32m2+7 |
| (1+m2)2 |
| 9 |
| (1+m2)2 |
所以d≥
| ||
| 2 |
所以△AOB面积S=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
点评:本题考查平面向量的数量积、三角形的面积公式,考查学生的运算求解能力、解决问题的能力.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
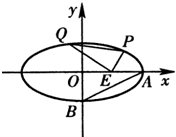 如图,已知中心在原点O、焦点在x轴上的椭圆C的离心率为
如图,已知中心在原点O、焦点在x轴上的椭圆C的离心率为