题目内容
如图在三棱锥P-ABC中,PA=PB=PC=13,∠ABC=90°,AB=8,BC=6,M为AC的中点.(1)求证:PM⊥平面ABC;
(2)求直线BP与平面ABC所成的角的正切值.
(3)求三棱锥P-ABC的体积.

【答案】分析:(1)作PO⊥平面ABC于点O,由PA=PB=PC,知O为△ABC的外心,由∠ABC=90°,知O为AC边的中点,即O与M点重合,由此能够证明PM⊥平面ABC;
(2)由(1)知PM⊥平面ABC,连结MB,则∠PBM就是直线BP与平面ABC所成的角,在直角三角形PBM中,利用边与角的关系即可求出答案.
(3)直接利用锥体的体积公式V= •S△ABC•PM即可得出答案.
•S△ABC•PM即可得出答案.
解答: 证明:(1)作PO⊥平面ABC于点O,
证明:(1)作PO⊥平面ABC于点O,
∵PA=PB=PC,
∴OA=OB=OC,即O为△ABC的外心
又∵△ABC中,∠ABC=90°,∴O为AC边的中点,
∴O与M点重合,
∴PM⊥平面ABC;
(2)连结MB,则∠PBM就是直线BP与平面ABC所成的角,
在直角三角形PBM中,PB=13,PM=12,BM= AC=5
AC=5
∴tan∠PBM= ;
;
(2)三棱锥P-ABC的体积V= •S△ABC•PM=
•S△ABC•PM= =96.
=96.
点评:本题考查直线与平面垂直的判定,考查直线与平面所成的角的求法,解题时要认真审题,仔细解答.
(2)由(1)知PM⊥平面ABC,连结MB,则∠PBM就是直线BP与平面ABC所成的角,在直角三角形PBM中,利用边与角的关系即可求出答案.
(3)直接利用锥体的体积公式V=
 •S△ABC•PM即可得出答案.
•S△ABC•PM即可得出答案.解答:
 证明:(1)作PO⊥平面ABC于点O,
证明:(1)作PO⊥平面ABC于点O,∵PA=PB=PC,
∴OA=OB=OC,即O为△ABC的外心
又∵△ABC中,∠ABC=90°,∴O为AC边的中点,
∴O与M点重合,
∴PM⊥平面ABC;
(2)连结MB,则∠PBM就是直线BP与平面ABC所成的角,
在直角三角形PBM中,PB=13,PM=12,BM=
 AC=5
AC=5∴tan∠PBM=
 ;
;(2)三棱锥P-ABC的体积V=
 •S△ABC•PM=
•S△ABC•PM= =96.
=96.点评:本题考查直线与平面垂直的判定,考查直线与平面所成的角的求法,解题时要认真审题,仔细解答.

练习册系列答案
相关题目
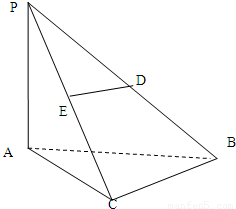
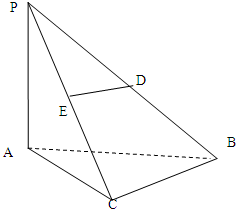 如图在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC,
如图在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC,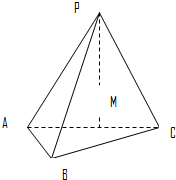 如图在三棱锥P-ABC中,PA=PB=PC=13,∠ABC=90°,AB=8,BC=6,M为AC的中点.
如图在三棱锥P-ABC中,PA=PB=PC=13,∠ABC=90°,AB=8,BC=6,M为AC的中点. 如图在三棱锥P-ABC中,AB⊥PC,AC=2,BC=4,
如图在三棱锥P-ABC中,AB⊥PC,AC=2,BC=4,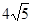
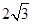 ,求二面角A-PB-C的平面角的余弦值.
,求二面角A-PB-C的平面角的余弦值.