题目内容
一个多面体的直观图及三视图如图所示:(其中M、N别是AF、BC的中点).
(I)求证:MN//平面CDEF;
(Ⅱ)求二面角D-MN-B的余弦值绝对值.

 三视图
三视图
解:由三视图可知,该多面体是底面为直角三角形的直三棱住ADE―BCF,
且AB=BC=BF=2,DE=CF=2![]()
∴∠CBF=![]()
 (I)取BF中点G,连MG、NG,由M、N分别为AF、BC
(I)取BF中点G,连MG、NG,由M、N分别为AF、BC
的中点可得,NG∥CF,MG∥EF,
∴平面MNG∥平面CDEF,
∴MN∥平面CDEF.
(II)建立空间直角坐标系,如图,
则A(0,0,0),B(2,0,0),D(0,0,2),F(2,2,0)
M(1,1,0),C(2,0,2),N(2,0,1),![]()
![]() ,
,![]()
设平面DMN的法向量![]()
则![]() ,
,
则![]()
![]() ;
;
设平面MNB的法向量为![]()
![]()

设二面角D―MN―B的平面角为![]() ,则
,则

∴二面角D―MN―B的余弦的绝对值为![]()

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 18、一个多面体的直观图及三视图如图所示,M、N分别是AB1、A1C1的中点.
18、一个多面体的直观图及三视图如图所示,M、N分别是AB1、A1C1的中点.
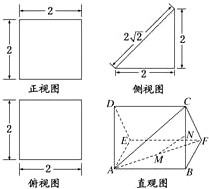 一个多面体的直观图及三视图如图所示:(其中M,N分别是AF,BC的中点).
一个多面体的直观图及三视图如图所示:(其中M,N分别是AF,BC的中点).

