Question

下列集合A到集合B的对应f是映射的共有几个
①A={-1，0，1}，B={-1，0，1}，f：x→y=x²；
②A={0，1}，B={-1，0，1}，f：x→y=；
③A=R，B=R，；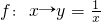
④A={x|x是衡水中学的班级}，B={x|x是衡水中学的学生}，对应关系f：每一个班级都对应班里的学生．

1. A.
   1
2. B.
   2
3. C.
   3
4. D.
   4

Answer 1

B
分析：根据映射的概念，对于集合A中的每一个元素在集合B中都有唯一的元素与它对应，观察几个对应，从而得到四个所述的对应是否是映射．
解答：根据映射的概念：对于集合A中的每一个元素在集合B中都有唯一的元素与它对应，是映射．
考察①②③④四个集合A到集合B的对应f：
对于①、②，对于集合A中的每一个元素在集合B中都有唯一的元素与它对应，它们都是映射；
对于选项③，集合A中的元素0在集合B中没有元素对应，不是映射；
对于选项④，由于衡水中学的学生可以在衡水中学的不同的班级，故集合B中的元素可能在集合A中有几个元素对应，不是映射；
∴是映射的共有2个．
故选B．
点评：本题考查映射的意义，考查判断一个对应是不是映射，本题还考查一些特殊的数字的特殊的特点，本题是一个基础题．