题目内容
下列集合A到集合B的对应f是映射的个数是
(1)A=Z,B=Q,f:A中数的倒数;
(2)A=N,B=N*,f:x→|x-1|;
(3)A=
(4)A={0,1},B={-1,0,1},f:A中数的倒数
- A.0个
- B.1个
- C.2个
- D.3个
B
分析:利用映射的定义逐个判断即可.
解答:由映射的定义知:对集合A中的每一个元素,按对应关系f,在集合B中都有唯一的元素与之对应,则f是集合A到集合B的映射.
对于(1)集合A中元素0没有倒数,因此在集合B中没有元素与之对应,所以(1)不是映射.
对于(2)集合A中元素1→|1-1|=0,但是0不在集合B中,所以(2)不是映射.
对于(3)集合A中每一个元素x≥3,按对应关系f:x→y= ,在集合B中都有唯一的元素与之对应,所以(3)是映射
,在集合B中都有唯一的元素与之对应,所以(3)是映射
对于(4)集合A中元素0没有倒数,故在集合B中没有元素与之对应,所以(4)不是映射.
故选B
点评:本题考查对映射概念的理解与把握,充分理解映射的概念是解题的关键.
分析:利用映射的定义逐个判断即可.
解答:由映射的定义知:对集合A中的每一个元素,按对应关系f,在集合B中都有唯一的元素与之对应,则f是集合A到集合B的映射.
对于(1)集合A中元素0没有倒数,因此在集合B中没有元素与之对应,所以(1)不是映射.
对于(2)集合A中元素1→|1-1|=0,但是0不在集合B中,所以(2)不是映射.
对于(3)集合A中每一个元素x≥3,按对应关系f:x→y=
 ,在集合B中都有唯一的元素与之对应,所以(3)是映射
,在集合B中都有唯一的元素与之对应,所以(3)是映射对于(4)集合A中元素0没有倒数,故在集合B中没有元素与之对应,所以(4)不是映射.
故选B
点评:本题考查对映射概念的理解与把握,充分理解映射的概念是解题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
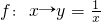 ,x∈A,y∈B.
,x∈A,y∈B.