题目内容
由函数y=f(x)确定数列{an},an=f(n),若函数y=f(x)的反函数y=f-1(x)能确定数列{bn},bn=f-1(n),则称数列{bn}是数列{an}的“反数列”.(1)已知函数f(x)=2
的反函数为f-1(x)=
(x≥0),则由函数f(x)=2
确定的数列{an}的反数列为{bn},求{bn}的通项公式;不等式
+
+…+
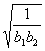≥1-2a对任意的正整数n恒成立,求实数a的范围;
(2)设函数y=3x确定的数列为{cn},{cn}的反数列为{dn},{cn}与{dn}的公共项组成的数列为{tn},求数列{tn}的前n项和Sn.
解:(1)f(x)=2(x≥0)an=2(n为正整数),f-1(x)=(x≥0).
∴数列{an}的反数列为{bn}的通项bn=(n为正整数).
∵+
+…+
=4［
+
+…+
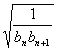］=4(1
),
∴{1
}单调递增.∴当n=1时,{1
}的最小值为
.
∵1-2a≤2,∴a≥
.∴使不等式对于任意正整数n恒成立的a的取值范围是［
,+∞).
(2)设公共项tk=cp=dq(k、p、q为正整数),cn=3n,dn=log3n.
∴3p=log3q,则q=
.11分有{cn}
{dn},tn=3n.
∴{tn}的前n项和Sn=
(3n-1).
练习册系列答案
相关题目
、
、
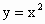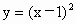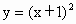的图象，并指出如何由函数
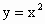的图象得到
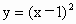与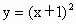
的图象；一般地，由函数f=f(x)的图象如何得到y=f(x＋a)的图象呢？类似地，由函数y=f(x)的图象如何得到y=f(x)＋a的图象呢？
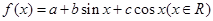的图像过点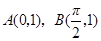
，且b>0，又
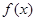的最大值为
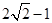，(1)求函数f(x)
的解析式；(2)由函数y= f (x)图像经过平移是否能得到一个奇函数y=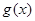
的图像？若能，请写出平移的过程；若不能，请说明理由。
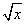确定数列{an}的反数列为{bn}，求{bn}的通项公式；
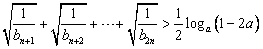对任意的正整数n恒成立，求实数a的取值范围；
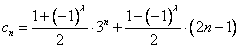（λ为正整数），若数列{cn}的反数列为{dn}，{cn}与{dn}的公共项组成的数列为{tn}， 求数列{tn}前n项和Sn。