题目内容
在锐角△ABC中,下列结论成立的是( )
| A.sinA>cosB | B.cosA>sinB | C.tanA>tanB | D.sinA>sinB |
锐角△ABC中,C为锐角,
∴A+B>
,
∴
>A>
-B>0,
A、正弦函数在(0,
)单调递增,
∴sinA>sin(
-B)=cosB,
本选项正确;
B、余弦函数在(0,
)单调递减,
cosA<cos(
-B)=sinB,
本选项错误;
C、正切函数在(0,
)单调递增,
∴tanA>tan(
-B)=cotB,
本选项错误;
D、根据正弦定理
=
得:当a>b时,sinA>sinB,
本选项不一定成立,
故选A
∴A+B>
| π |
| 2 |
∴
| π |
| 2 |
| π |
| 2 |
A、正弦函数在(0,
| π |
| 2 |
∴sinA>sin(
| π |
| 2 |
本选项正确;
B、余弦函数在(0,
| π |
| 2 |
cosA<cos(
| π |
| 2 |
本选项错误;
C、正切函数在(0,
| π |
| 2 |
∴tanA>tan(
| π |
| 2 |
本选项错误;
D、根据正弦定理
| a |
| sinA |
| b |
| sinB |
本选项不一定成立,
故选A

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
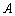 的对边长等于2,向量
的对边长等于2,向量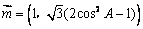 ,向量
,向量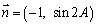 .
.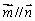 ,求锐角A的大小;
,求锐角A的大小;