Question

 

△ABC中，锐角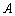的对边长等于2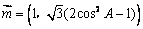，向量，向量.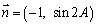

（Ⅰ）若向量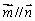，求锐角A的大小；

（Ⅱ）在（Ⅰ）的条件下，求△ABC面积的最大值．   

 

 

 

 

 

 

 

 

 

Answer 1

【答案】

 解：（1）  . ………2分

 即

  为锐角   

                                                 ……………5 分

即A＝时

故当时角A＝.                                        ……………7 分

（2）设角A、B、C所对的边长分别为a、b、c，

    由余弦定理，得 b²＋c²－a²＝2bccosA，                 ……………9 分

    即bc＋4＝b²＋c²≥2bc，                               ……………11分

    所以bc≤4，当且仅当b＝c＝2时取等号.                  

又S_△ABC＝bcsinA＝bc≤.                            ……………14分

当且仅当a＝b＝c＝2时，△ABC的面积最大为.                   ……………15分