题目内容
设A={(x,y)|2x=y-5},B={(x,y)|1-2x=y},则A∩B=________.
{(-1,3)}
分析:因为集合A,B分别表示两条直线上的点的集合,所以A∩B表示直线2x=y-5上与直线1-2x=y的交点构成的集合,联立两直线方程,解方程组,可得两直线交点,则A∩B可求.
解答:解;∵集合A表示直线2x=y-5上所有点的集合,集合B表示直线1-2x=y上所有点的集合
∴A∩B表示直线2x=y-5上与直线1-2x=y的交点的集合
由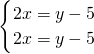 可得,
可得,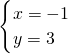
∴直线2x=y-5上与直线1-2x=y的交点坐标为(-1,3)
故答案为{(-1,3)}
点评:本题主要考查了集合的描述法,以及集合交集的运算,属于集合的常规题
分析:因为集合A,B分别表示两条直线上的点的集合,所以A∩B表示直线2x=y-5上与直线1-2x=y的交点构成的集合,联立两直线方程,解方程组,可得两直线交点,则A∩B可求.
解答:解;∵集合A表示直线2x=y-5上所有点的集合,集合B表示直线1-2x=y上所有点的集合
∴A∩B表示直线2x=y-5上与直线1-2x=y的交点的集合
由
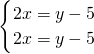 可得,
可得,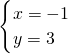
∴直线2x=y-5上与直线1-2x=y的交点坐标为(-1,3)
故答案为{(-1,3)}
点评:本题主要考查了集合的描述法,以及集合交集的运算,属于集合的常规题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目