题目内容
（10分）
中山市的一家报刊摊点，从报社买进《中山日报》的价格是每份0.60元，卖出的价格是每份1元，卖不掉的报纸
可以以每份0.1元的价格退回报社。在一个月（以30天计算）里，有20天每天可卖出400份，其余10天每天只能卖出250份，但每天
从报社买进的份数必须相同，这个推主每天从报社买进多少份，才能使每月所获的利润最
大？并计算他一个月最多可赚得多少
元？
中山市的一家报刊摊点，从报社买进《中山日报》的价格是每份0.60元，卖出的价格是每份1元，卖不掉的报纸
可以以每份0.1元的价格退回报社。在一个月（以30天计算）里，有20天每天可卖出400份，其余10天每天只能卖出250份，但每天从报社买进的份数必须相同，这个推主每天从报社买进多少份，才能使每月所获的利润最大？并计算他一个月最多可赚得多少元？买进400份报纸可获得最大利润，最大利润为3315元。
解:设这个摊主每天从报社买进
份报纸，每月所获的利润为
元，则由题意可知
,且
=
∵ 函数
在[250，40
0]上单调递增，∴当x=400时，y最大=3315，即摊主每天从报社买进400份报纸可获得最大利润，最大利润为3315元。
份报纸，每月所获的利润为元，则由题意可知,且=
∵ 函数
在[250，400]上单调递增，∴当x=400时，y最大=3315，即摊主每天从报社买进400份报纸可获得最大利润，最大利润为3315元。
练习册系列答案
快乐5加2金卷系列答案
相关题目
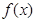是定义在
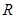上以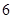
为周期的函数，
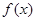在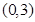
内单调递减，且
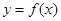的图象关于直线
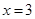对称，则下面正确的结论是（ ）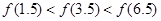
，
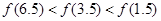
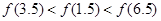
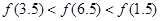
，当甲公司投入
万元作宣传时，若乙公司投入的宣传费小于
万元，则乙公司对这一新产品的开发有失败的风险，否则没有失败的风险；当乙公
万元，则甲公司对这一新产品的开发有失败的风险，否则没有失败的风险．
费用，问甲、乙两公司应投入多少宣传费？
在定义域内是增函数；③函数
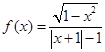图象关于原点对称；④既是奇函数又是偶函数的函数一定是
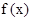="0"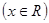 
; ⑤函数y＝f(x＋2)图象与函数y＝f(2－x)图象关于直线x＝2对称；其中正确命题的个数为：（ ）
的单调递减区间是 .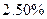 
保持不变，到2015年9月1日将所有的存款和利息全部取出，他可取回的钱数约为 
【 】
上选择一点P建造垃圾处理厂，其中
。已知垃圾处理厂对城市的影响度与所选地点到城市的距离有关，对城A和城B的总影响度为对城A和城B的影响度之和。统计调查表明：垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比，比例系数为4；对城B的影响度与所选地点到城B的距离的平方成反比，比例系数为9。记垃圾处理厂对城A和城B的总影响度为y，设AP=xkm，
的函数关系，并求该函数的定义域和值域；
有解，则
________________。