题目内容
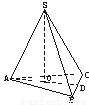
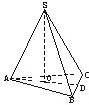 如图,设三棱锥S-ABC的三个侧棱与底面ABC所成的角都是60°,又∠BAC=60°,且SA⊥BC.
如图,设三棱锥S-ABC的三个侧棱与底面ABC所成的角都是60°,又∠BAC=60°,且SA⊥BC.(1)求证:S-ABC为正三棱锥;
(2)已知SA=a,求S-ABC的全面积.
分析:(1)利用已知条件,证明底面三角形是正三角形,证明顶点S在底面的射影是底面的中心,就证明S-ABC为正三棱锥;
(2)SA=a,只要求出正三棱锥S-ABC的侧高SD与底面边长,即可求S-ABC的全面积.
(2)SA=a,只要求出正三棱锥S-ABC的侧高SD与底面边长,即可求S-ABC的全面积.
解答:(1)证明:正棱锥的定义中,底面是正多边形;
顶点在底面上的射影是底面的中心,两个条件缺一不可.
作三棱锥S-ABC的高SO,O为垂足,连接AO并延长交BC于D.
因为SA⊥BC,所以AD⊥BC.又侧棱与底面所成的角都相等,
从而O为△ABC的外心,OD为BC的垂直平分线,所以AB=AC.又∠BAC=60°,
故△ABC为正三角形,且O为其中心.所以S-ABC为正三棱锥.
(2)解:在Rt△SAO中,由于SA=a,∠SAO=60°,
所以SO=
a,AO=
a.因O为重心,所以AD=
AO=
a,
BC=2BD=2ADcot60°=
a,OD=
AD=
a.
在Rt△SOD中,SD2=SO2+OD2=(
a)2+(
a)2=
,则SD=
a.
于是,(SS-ABC)全=
•(
a)2sin60°+3•
•
a•
a=
a2.
顶点在底面上的射影是底面的中心,两个条件缺一不可.
作三棱锥S-ABC的高SO,O为垂足,连接AO并延长交BC于D.
因为SA⊥BC,所以AD⊥BC.又侧棱与底面所成的角都相等,
从而O为△ABC的外心,OD为BC的垂直平分线,所以AB=AC.又∠BAC=60°,
故△ABC为正三角形,且O为其中心.所以S-ABC为正三棱锥.
(2)解:在Rt△SAO中,由于SA=a,∠SAO=60°,
所以SO=
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
BC=2BD=2ADcot60°=
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
在Rt△SOD中,SD2=SO2+OD2=(
| ||
| 2 |
| 1 |
| 4 |
| 13 |
| 16 |
| ||
| 14 |
于是,(SS-ABC)全=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| ||
| 2 |
3(
| ||||
| 16 |
点评:本题考查棱锥的结构特征,棱柱、棱锥、棱台的侧面积和表面积,考查计算能力,逻辑思维能力,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2,
如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2, C.
C. (2010•上饶二模)如图,设三棱锥O-ABC的三条侧棱OA,OB,OC两两垂直,三个侧面与底面所成的二面角O-AB-C,O-BC-A,O-CA-B分别等于α1,α2,α3.记△OAB,△OBC,△OCA,△ABC的面积分别为S1,S2,S3,S,则下列四个命题:(1)Si=Scosαi(i=1,2,3)(2)若∠BAO=∠CAO=45°,则∠BAC=60°(3)S2=S12+S22+S32.(4)α1,α2,α3的取值可以分别是30°,45°,60°.
(2010•上饶二模)如图,设三棱锥O-ABC的三条侧棱OA,OB,OC两两垂直,三个侧面与底面所成的二面角O-AB-C,O-BC-A,O-CA-B分别等于α1,α2,α3.记△OAB,△OBC,△OCA,△ABC的面积分别为S1,S2,S3,S,则下列四个命题:(1)Si=Scosαi(i=1,2,3)(2)若∠BAO=∠CAO=45°,则∠BAC=60°(3)S2=S12+S22+S32.(4)α1,α2,α3的取值可以分别是30°,45°,60°.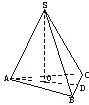 如图,设三棱锥S-ABC的三个侧棱与底面ABC所成的角都是60°,又∠BAC=60°,且SA⊥BC.
如图,设三棱锥S-ABC的三个侧棱与底面ABC所成的角都是60°,又∠BAC=60°,且SA⊥BC.