题目内容
 如图所示,设M,N为△ABC内的两点,且
如图所示,设M,N为△ABC内的两点,且| AM |
| 1 |
| 4 |
| AB |
| 1 |
| 3 |
| AC |
| AN |
| 2 |
| 5 |
| AB |
| 1 |
| 2 |
| AC |
分析:先根据题意画出图形,然后根据△ABM与△ABN的面积之比等于高之比,转化成AP与AQ之比,从而求出所求.
解答:解:根据
=
+
,
=
+
画出图形如下:
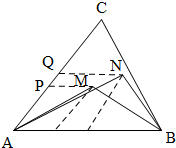
∵AP=
AC,AQ=
AC,
∴
=
=
=
=
=
.
故答案为:
.
| AM |
| 1 |
| 4 |
| AB |
| 1 |
| 3 |
| AC |
| AN |
| 2 |
| 5 |
| AB |
| 1 |
| 2 |
| AC |

∵AP=
| 1 |
| 3 |
| 1 |
| 2 |
∴
| S△ABM |
| S△ABN |
| ||
|
| h1 |
| h2 |
| AP |
| AQ |
| ||
|
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:本题主要考查了向量在几何中的应用,解题的关键就是画出图形,同时考查了分析问题的能力,属于中档题.

练习册系列答案
相关题目
 据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(单位:h)的函数图象如图所示,设t时刻沙尘暴所经过的路程为S(t).
据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(单位:h)的函数图象如图所示,设t时刻沙尘暴所经过的路程为S(t).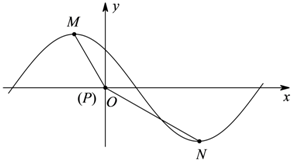 (2012•焦作模拟)函数y=
(2012•焦作模拟)函数y=