题目内容
一动圆与两圆x2+y2=1和x2+y2-8x+12=0都相外切,则动圆圆心的轨迹为
- A.圆
- B.椭圆
- C.双曲线的一支
- D.抛物线
C
记圆x2+y2-8x+12=0的圆心为F,
设动圆圆心为M,半径为r,
由题设条件知,
|MF|=r+2,|MO|=r+1,
两式相减得|MF|-|MO|=1,
根据双曲线定义,点M的轨迹是以O、F为焦点,实轴长为1的双曲线的一支.
记圆x2+y2-8x+12=0的圆心为F,
设动圆圆心为M,半径为r,
由题设条件知,
|MF|=r+2,|MO|=r+1,
两式相减得|MF|-|MO|=1,
根据双曲线定义,点M的轨迹是以O、F为焦点,实轴长为1的双曲线的一支.

练习册系列答案
相关题目
 下列四个命题中,真命题的序号有
下列四个命题中,真命题的序号有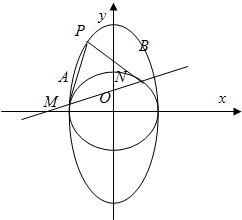 附加题:如图,过椭圆C:
附加题:如图,过椭圆C: (写出所有真命题的序号).
(写出所有真命题的序号). ②圆x2+y2+4x+2y+1=0与直线y=
②圆x2+y2+4x+2y+1=0与直线y= 相交,所得弦长为2.
相交,所得弦长为2. +
+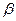 )=
)= ,si
,si n(
n(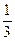 ,则tan
,则tan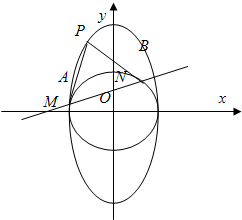 附加题:如图,过椭圆C:
附加题:如图,过椭圆C: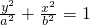 (a>b>0)上一动点P引圆x2+y2=b2的两条切线PA,PB(A,B为切点).直线AB与x轴、y轴分别交于M、N两点.
(a>b>0)上一动点P引圆x2+y2=b2的两条切线PA,PB(A,B为切点).直线AB与x轴、y轴分别交于M、N两点.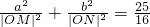 ,求椭圆C的方程;
,求椭圆C的方程;