题目内容
正四棱锥V-ABCD中,底面正方形的边长为2,侧棱长为
,E为侧棱VA的中点,则EC与底面ABCD所成角的正切值为( )
| 3 |
分析:先根据条件得到V在底面ABCD中的射影为底面中心O;取AO中点F进而得到∠ECF即为EC与底面ABCD所成角;再通过求边长即可得到结论.
解答:解:由题得:V在底面ABCD中的射影为底面中心O.
 .
.
取AO中点F,连接EF,则EF∥VO
∴EF⊥底面ABCD,
∠ECF即为EC与底面ABCD所成角
因为底面正方形的边长为2⇒AC=2
,
故VO=
=
=1.
∴EF=
VO=
.
则FC=OC+FO=
+
=
.
∴tan∠ECF=
=
=
.
故EC与底面ABCD所成角的正切值为:
.
故选B
 .
.取AO中点F,连接EF,则EF∥VO
∴EF⊥底面ABCD,
∠ECF即为EC与底面ABCD所成角
因为底面正方形的边长为2⇒AC=2
| 2 |
故VO=
| VC2-OC2 |
(
|
∴EF=
| 1 |
| 2 |
| 1 |
| 2 |
则FC=OC+FO=
| 2 |
| ||
| 2 |
3
| ||
| 2 |
∴tan∠ECF=
| EF |
| FC |
| ||||
|
| ||
| 6 |
故EC与底面ABCD所成角的正切值为:
| ||
| 6 |
故选B
点评:本题考查直线与平面所成角的正切值的求法,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB;已知VA=kAB,点E是VC的中点,底面正方形ABCD边长为2a,高为h.
如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB;已知VA=kAB,点E是VC的中点,底面正方形ABCD边长为2a,高为h.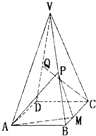 (2013•乌鲁木齐一模)在正四棱锥V-ABCD中,P,Q分别为棱VB,VD的中点,点 M 在边 BC 上,且 BM:BC=1:3,AB=2
(2013•乌鲁木齐一模)在正四棱锥V-ABCD中,P,Q分别为棱VB,VD的中点,点 M 在边 BC 上,且 BM:BC=1:3,AB=2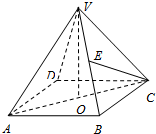 (2009•虹口区一模)如图,正四棱锥V-ABCD的高和底面的边长均相等,E是棱VB的中点.
(2009•虹口区一模)如图,正四棱锥V-ABCD的高和底面的边长均相等,E是棱VB的中点.