题目内容
(本小题满分12分) 已知向量 ,
,
⑴求函数 的最小正周期;
的最小正周期;
⑵若 ,求函数
,求函数 的单调递增区间.
的单调递增区间.
(1)最小正周期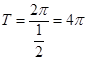 ;(2)
;(2) 的单调递增区间是
的单调递增区间是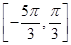 。
。
解析试题分析:(1)根据降幂公式和和角公式,把f(x)化成正弦型函数再求最小正周期
(2)利用整体代换思想求原函数的单调增区间
解: ∵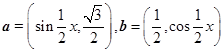
∴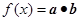
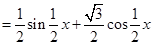 ……2分
……2分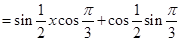 ……3分
……3分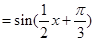 ……4分
……4分
(1) ∵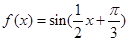 ,∴函数
,∴函数 的最小正周期
的最小正周期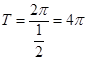 ……5分
……5分
(2)∵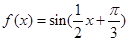 ,令
,令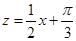 ,函数
,函数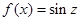 的单调区间是
的单调区间是 ,
,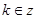 ……6分
……6分
由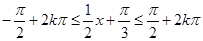 ,
,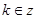
得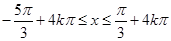 ,
,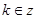 ……9分
……9分
取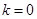 ,得
,得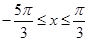 ……10分
……10分
而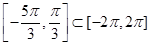 ……11分
……11分
因此,当 时,函数
时,函数 的单调递增区间是
的单调递增区间是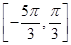 ……12分考点:本试题主要考查了三角函数的性质,要求熟练掌握正弦函数的性质,同时考查向量的数量积和整体代换思想.是三角函数和向量的交汇题型.属简单题。
……12分考点:本试题主要考查了三角函数的性质,要求熟练掌握正弦函数的性质,同时考查向量的数量积和整体代换思想.是三角函数和向量的交汇题型.属简单题。
点评:解决该试题的关键是将所求的函数关系式,结合向量的数量积公式化为单一三角函数,同时能利用周期公式得到周期,利用正弦函数的单调区间,整体代换得到所求解函数的单调增区间。

练习册系列答案
相关题目
已知 ,
, ,若
,若 为满足
为满足 的一随机整数,则
的一随机整数,则 是直角三角形的概率为( )
是直角三角形的概率为( )
A. | B. | C. | D. |
已知 ,
, ,
, 为坐标原点,点C在∠AOB内,且
为坐标原点,点C在∠AOB内,且 ,设
,设 ,则
,则 的值为( )
的值为( )
A. | B.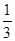 | C. | D. |

 的值;
的值;  ,且
,且 ,求
,求 的值.
的值. ,
,  是平面上一动点,
是平面上一动点, 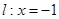 上的射影为点
上的射影为点 ,且满足
,且满足
 的方程;
的方程;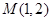 作曲线
作曲线 , 设
, 设 , 当
, 当 时,证明直线
时,证明直线 恒过定点,并求出该定点坐标.
恒过定点,并求出该定点坐标. 中,
中, 为
为 的中点,
的中点, 分别在
分别在 上,且
上,且
 ,求
,求 的值。
的值。 ,则G是
,则G是 ,点M是
,点M是 ,则点P在边BC的垂线上;
,则点P在边BC的垂线上; 满足
满足 ,若
,若 ,
, 且
且 满足:
满足: ,
, ,
, 为
为 。
。 ,
,
 时,求
时,求 的取值集合; (2)求函数
的取值集合; (2)求函数 的单调递增区间
的单调递增区间