题目内容
已知△ABC中,b2=ac
(1)求证: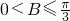
(2)求 的值域.
的值域.
解:(1)证明:因为cosB= =
= ≥
≥ =
= ,
,
0<B<π
∴0<B≤ .
.
(2)∵ =
= =sinB+cosB=
=sinB+cosB= sin(B+
sin(B+ )
)
又∵0<B≤
∴ <B+
<B+ ≤
≤
∴ <sin(B+
<sin(B+ )≤1
)≤1
∴1<y .
.
即 的值域为(1,
的值域为(1, ].
].
分析:(1)先利用余弦定理表示出cosB,再结合b2=ac求出cosB的范围即可证明结论;
(2)先对所求的函数进行化简,再结合第一问的结论以及辅助角公式的运用即可求出 的值域.
的值域.
点评:本题主要考查余弦定理的运用以及辅助角公式的运用.一般在三角形中求角的范围问题时,比较常用余弦定理.
 =
= ≥
≥ =
= ,
,0<B<π
∴0<B≤
 .
.(2)∵
 =
= =sinB+cosB=
=sinB+cosB= sin(B+
sin(B+ )
)又∵0<B≤

∴
 <B+
<B+ ≤
≤
∴
 <sin(B+
<sin(B+ )≤1
)≤1∴1<y
 .
.即
 的值域为(1,
的值域为(1, ].
].分析:(1)先利用余弦定理表示出cosB,再结合b2=ac求出cosB的范围即可证明结论;
(2)先对所求的函数进行化简,再结合第一问的结论以及辅助角公式的运用即可求出
 的值域.
的值域.点评:本题主要考查余弦定理的运用以及辅助角公式的运用.一般在三角形中求角的范围问题时,比较常用余弦定理.

练习册系列答案
相关题目

 的值域.
的值域.