题目内容
设正项数列{an}的前n项和是Sn,若{an}和{ }都是等差数列,且公差相等,则a1=________.
}都是等差数列,且公差相等,则a1=________.

分析:设公差为d,首项a1,利用等差中项的概念列关系,通过两次平方运算及可求得答案.
解答:设公差为d,首项a1
∵{an},{
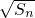 }都是等差数列,且公差相等,
}都是等差数列,且公差相等,∴2
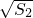 =
= +
+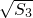 ,
,即2
 =
=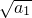 +
+ ,
,两端平方得:4(2a1+d)=a1+3a1+3d+2
 ,
,4a1+d=2
 ,
,两端再平方得:16
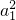 +8a1d+d2=4a1(3a1+3d),
+8a1d+d2=4a1(3a1+3d),∴4
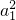 -4a1d+d2=0,
-4a1d+d2=0,d=2a1,又两数列公差相等,
∴
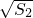 -
- =a2-a1=d=2a1,
=a2-a1=d=2a1,即
 -
-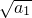 =2a1,
=2a1,解得:
2
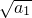 =1,
=1,∴a1=
 或a1=0({an}为正项数列,故舍)
或a1=0({an}为正项数列,故舍)∴a1=
 .
.故答案为:
 .
.点评:本题考查等差数列的性质,考查等差中项的性质,考查化归与方程思想,属于难题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目