题目内容
 如图,倾斜角为α的直线经过抛物线y2=8x的焦点F,且与抛物线交于A、B两点.
如图,倾斜角为α的直线经过抛物线y2=8x的焦点F,且与抛物线交于A、B两点.(1)求抛物线的焦点F的坐标及准线l的方程;
(2)若α为锐角,作线段AB的垂直平分线m交x轴于点P,证明|FP|-|FP|cos2α为定值,并求此定值.
分析:(1)根据抛物线的标准方程,可求抛物线的焦点F的坐标及准线l的方程;
(2)作AC⊥l,BD⊥l,垂足为C,D,求出|FA|,|FB|,即可得到结论.
(2)作AC⊥l,BD⊥l,垂足为C,D,求出|FA|,|FB|,即可得到结论.
解答:(1)解:设抛物线C:y2=2px(p>0),则2p=8,从而p=4
因此焦点F(2,0),准线方程为x=-2;
(2)证明:作AC⊥l,BD⊥l,垂足为C,D.
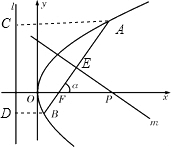
则由抛物线的定义,可得|FA|=|AC|,|FB|=|BD|
设A(x1,y1),B(x2,y2),则|FA|=|AC|=|FA|cosα+4,∴|FA|=
同理|FB|=
记直线m与AB的交点为E,则|FE|=|FA|-|AE|=|FA|-
=
(|FA|-|FB|)=
∴|FP|=
=
∴|FP|-|FP|cos2α=
(1-cos2α)=8.
因此焦点F(2,0),准线方程为x=-2;
(2)证明:作AC⊥l,BD⊥l,垂足为C,D.

则由抛物线的定义,可得|FA|=|AC|,|FB|=|BD|
设A(x1,y1),B(x2,y2),则|FA|=|AC|=|FA|cosα+4,∴|FA|=
| 4 |
| 1-cosα |
同理|FB|=
| 4 |
| 1+cosα |
记直线m与AB的交点为E,则|FE|=|FA|-|AE|=|FA|-
| |FA|+|FB| |
| 2 |
| 1 |
| 2 |
| 4cosα |
| sin2α |
∴|FP|=
| |FE| |
| cosα |
| 4 |
| sin2α |
∴|FP|-|FP|cos2α=
| 4 |
| sin2α |
点评:本题考查抛物线的几何性质,考查抛物线的定义,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,倾斜角为α的直线经过抛物线y2=4x的焦点,且与抛物线交于A、B两点,Q为A、B中点,
如图,倾斜角为α的直线经过抛物线y2=4x的焦点,且与抛物线交于A、B两点,Q为A、B中点, (2013•安庆三模)如图,倾斜角为θ的直线OP与单位圆在第一象限的部分交于点P,单位圆与坐标轴交于点A(-1,0),点B(0,-1),PA与y轴交于点N,PB与x轴交于点M,设
(2013•安庆三模)如图,倾斜角为θ的直线OP与单位圆在第一象限的部分交于点P,单位圆与坐标轴交于点A(-1,0),点B(0,-1),PA与y轴交于点N,PB与x轴交于点M,设
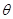 的直线
的直线 与单位圆在第一象限的部分交于点
与单位圆在第一象限的部分交于点 ,单位圆与坐标轴交于点
,单位圆与坐标轴交于点 ,点
,点 ,
, 与
与 轴交于点
轴交于点 ,
, 与
与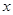 轴交于点
轴交于点 ,设
,设


 的最小值.
的最小值.