题目内容
已知数列{an}满足Sn+an=2n+1.
(1)写出a1, a2, a3,并推测an的表达式;
(2)用数学归纳法证明所得的结论.
解:(1) a1= , a2=
, a2= , a3=
, a3= , 猜测 an=2-
, 猜测 an=2-
(2) ①由(1)已得当n=1时,命题成立;
②假设n=k时,命题成立,即 ak=2- ,
,
当n=k+1时, a1+a2+……+ak+ak+1+ak+1=2(k+1)+1,
且a1+a2+……+ak=2k+1-ak
∴2k+1-ak+2ak+1=2(k+1)+1=2k+3,
∴2ak+1=2+2- , ak+1=2-
, ak+1=2- ,
,
即当n=k+1时,命题成立. 根据①②得n∈N+ , an=2- 都成立。
都成立。

练习册系列答案
相关题目
 在
在 上单调递增,则实数
上单调递增,则实数 的取值范围是 .
的取值范围是 . 其中
其中 ,
, 是
是 的小数点后第n位数字,例如
的小数点后第n位数字,例如 ,则
,则 (共2013个f)= .
(共2013个f)= . 为角
为角 终边上一点,则cos
终边上一点,则cos B.
B. C.
C. D.
D.
 B.50
B.50  ,
, ,则
,则 在复平面内对应的点位于( )
在复平面内对应的点位于( )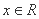 ,则“
,则“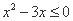 ”是“
”是“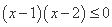 成立”的( )
成立”的( )