题目内容
正项等比数列{an}中,若a5•a6=4,则log2a1+log2a2+…+log2a10= .
考点:等比数列的性质
专题:计算题,等差数列与等比数列
分析:利用 等比数列的定义和性质,把要求的式子化为log2(a5a6)5,把条件代入并利用对数的运算性质求出结果.
解答:
解:∵等比数列{an}各项均为正数,a5a6=4,
∴根据对数的运算性质,得
log2a1+log2a2+…+log2a10=log2(a1a2a3…a9a10)=log2(a5a6)5=log2(4)5=10
故答案为:10.
∴根据对数的运算性质,得
log2a1+log2a2+…+log2a10=log2(a1a2a3…a9a10)=log2(a5a6)5=log2(4)5=10
故答案为:10.
点评:本题考查了等比数列的性质和对数的运算性质,考查了转化化归的数学思想,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( )
| A、若m∥α,n∥α,则m∥n |
| B、若α∥β,m?α,n?β,则m∥n |
| C、若α⊥β=m,n?α,则n⊥β |
| D、若m⊥α,m∥n,n?β,则α⊥β |
设某离散型随机变量ξ的概率分布列如下表,则p的值为( )
| ξ | 1 | 2 | 3 | 4 | ||||||
| P |
|
|
|
p |
A、
| ||
B、
| ||
C、
| ||
D、
|
 在平行六面休ABCD-A′B′C′D′中,若
在平行六面休ABCD-A′B′C′D′中,若| AC′ |
| AB |
| BC |
| C′C |
A、
| ||
B、
| ||
C、
| ||
D、
|
复数z=-1+i(i为虚数单位)在复平面上对应的点落在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
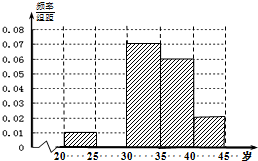 对某市“四城同创”活动中800名志愿者的年龄抽样调查统计后得到频率分布直方图(如图),但是年龄组为[25,30)的数据不慎丢失,则依据此图可得:
对某市“四城同创”活动中800名志愿者的年龄抽样调查统计后得到频率分布直方图(如图),但是年龄组为[25,30)的数据不慎丢失,则依据此图可得: