题目内容
15.设M、N、T是椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1上三个点,M、N在直线x=8上的摄影分别为M1、N1.(Ⅰ)若直线MN过原点O,直线MT、NT斜率分别为k1,k2,求证k1k2为定值.
(Ⅱ)若M、N不是椭圆长轴的端点,点L坐标为(3,0),△M1N1L与△MNL面积之比为5,求MN中点K的轨迹方程.
分析 (Ⅰ)设M(p,q),N(-p,-q),T(x0,y0),则k1k2=$\frac{{{y}_{0}}^{2}-{q}^{2}}{{{x}_{0}}^{2}-{p}^{2}}$,
又$\frac{{p}^{2}}{16}+\frac{{q}^{2}}{12}=1,\frac{{{x}_{0}}^{2}}{16}+\frac{{{y}_{0}}^{2}}{12}=1$即可得k1k2
(Ⅱ)设直线MN与x轴相交于点R(r,0),根据面积之比得r
即直线MN经过点F(2,0).设M(x1,y1),N(x2,y2),K(x0,y0)
分①当直线MN垂直于x轴时,②当直线MN与x轴不垂直时,设MN的方程为y=k(x-2)
x0=$\frac{8{k}^{2}}{3+4{k}^{2}}$.${y}_{0}=\frac{-6k}{3+4{k}^{2}}$消去k,整理得(x0-1)2+$\frac{4{{y}_{0}}^{2}}{3}$=1(y0≠0).
解答 解:(Ⅰ)设M(p,q),N(-p,-q),T(x0,y0),则k1k2=$\frac{{{y}_{0}}^{2}-{q}^{2}}{{{x}_{0}}^{2}-{p}^{2}}$,…(2分)
又$\frac{{p}^{2}}{16}+\frac{{q}^{2}}{12}=1,\frac{{{x}_{0}}^{2}}{16}+\frac{{{y}_{0}}^{2}}{12}=1$两式相减得$\frac{{{x}_{0}}^{2}-{p}^{2}}{16}+\frac{{{y}_{0}}^{2}-{q}^{2}}{12}=0$,
即k1k2=$\frac{{{y}_{0}}^{2}-{q}^{2}}{{{x}_{0}}^{2}-{p}^{2}}$=-$\frac{3}{4}$,…(…(5分)
(Ⅱ)设直线MN与x轴相交于点R(r,0),s△MNL=$\frac{1}{2}$×|r-3|•|yM-yN|
${S}_{{M}_{1}{N}_{1}L}$=$\frac{1}{2}•5•$|${y}_{{M}_{1}}-{y}_{{N}_{1}}|\$.
由于△M1N1L与△MNL面积之比为5且|yM-yN|=|${y}_{{M}_{1}}-{y}_{{N}_{1}}|\$,得
$\frac{1}{2}•5•|{y}_{{M}_{1}}-{y}_{{N}_{1}}|\$=5$|r-3|•|{y}_{M}-{y}_{N}|\$$•\frac{1}{2}$,r=4(舍去)或r=2.…(8分)
即直线MN经过点F(2,0).设M(x1,y1),N(x2,y2),K(x0,y0)
①当直线MN垂直于x轴时,弦MN中点为F(2,0);…(9分)
②当直线MN与x轴不垂直时,设MN的方程为y=k(x-2),则
联立$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1,y=k(x-2)$.⇒(3+4k2)x2-16k2x+16k2-48=0
${x}_{1}+{x}_{2}=\frac{16{k}^{2}}{3+4{k}^{2}}$${x}_{1}{x}_{2}=\frac{16{k}^{2}-48}{3+4{k}^{2}}$.…(10分)
x0=$\frac{8{k}^{2}}{3+4{k}^{2}}$.${y}_{0}=\frac{-6k}{3+4{k}^{2}}$
消去k,整理得(x0-1)2+$\frac{4{{y}_{0}}^{2}}{3}$=1(y0≠0).
综上所述,点K的轨迹方程为(x-1)2+$\frac{4{y}^{2}}{3}$=1(x>0).…(12分)
点评 本题考查了轨迹方程的求法,及直线与椭圆的位置关系,属于中档题.

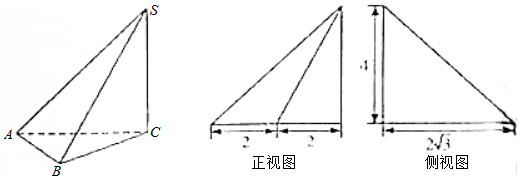
| A. | 32π | B. | $\frac{112π}{3}$ | C. | $\frac{28π}{3}$ | D. | $\frac{64}{3}$π |
| A. | [$\frac{π}{12}$,$\frac{7π}{12}$] | B. | [-$\frac{5π}{12}$,$\frac{π}{12}$] | C. | [-$\frac{π}{3}$,$\frac{2π}{3}$] | D. | [-$\frac{π}{6}$,$\frac{5π}{6}$] |
| A. | (2,+∞) | B. | $(0,\frac{1}{2})∪(2,+∞)$ | C. | $(0,\frac{{\sqrt{2}}}{2})∪(\sqrt{2},+∞)$ | D. | $(\sqrt{2},+∞)$ |