题目内容
【题目】如图1,矩形![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,以
的中点,以![]() 为折痕把
为折痕把![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且
的位置,且![]() ,如图2.
,如图2.
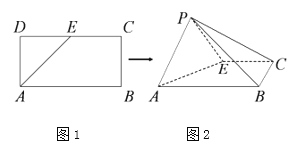
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)取BC的中点F,AE的中点O,连结![]() ,
,![]() ,
,![]() ,则可证
,则可证![]() 平面
平面![]() ,得出BC⊥PO,又PO⊥AE得出PO⊥平面ABCE,于是平面APE⊥平面ABCE.
,得出BC⊥PO,又PO⊥AE得出PO⊥平面ABCE,于是平面APE⊥平面ABCE.
(II)建立空间直角坐标系![]() ,求得平面
,求得平面![]() 的法向量为
的法向量为![]() , 设直线
, 设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,根据
,根据![]() 求解即可.
求解即可.
(Ⅰ)取![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,
由已知得,四边形![]() 是梯形,
是梯形,![]() ,
,![]()
∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]()
由已知得![]() ,∴
,∴![]() ,
,
又![]() 与
与![]() 相交∴
相交∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.

(II)建立空间直角坐标系![]() ,如图所示,设
,如图所示,设![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,
,
则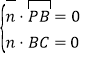 ,∴
,∴![]() ,取
,取![]() ,得
,得![]() ,
,
又![]() ,设直线
,设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
则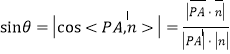
![]() .
.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
【题目】为了传承经典,促进学生课外阅读,某校从高中年级和初中年级各随机抽取100名学生进行有关对中国四大名著常识了解的竞赛,图1和图2分别是高中年级和初中年级参加竞赛的学生成绩按照![]() ,
,![]() ,
,![]() 分组,得到的频率分布直方图.
分组,得到的频率分布直方图.
(1)完成下列![]() 的列联表,并回答是否有
的列联表,并回答是否有![]() 的把握认为“两个学段的学生对四大名著的了解有差异”?
的把握认为“两个学段的学生对四大名著的了解有差异”?
成绩小于60分的人数 | 成绩不小于60的人数 | 合计 | |
初中年级 | |||
高中年级 | |||
合计 |
(2)规定竞赛成绩不少于70分的为优秀,按分层抽样的方法从高中,初中年级优秀学生中抽取5人进行复赛,在复赛人员中选3人进行面试,记面试人员中来自初中段的为随机变量X,求随机变量X的分布列与期望.
![]() 其中
其中![]()
附表:
| 0.10 | 0.05 | span>0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6635 | 10.828 |