题目内容
已知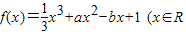 ,a、b为实数)有极值,且x=1处的切线与直线x-y+1=0平行.
,a、b为实数)有极值,且x=1处的切线与直线x-y+1=0平行.(1)求实数a的取值范围;
(2)若f(x)在(2,+∞)上是单增函数,求实数a的取值范围.
【答案】分析:(1)先求导函数f'(x),然后根据f'(1)=1可求出a与b的关系,再由f(x)有极值可知△>0,消去b可求出a的取值范围;
(2)根据f(x)在x>2上是单增函数则f'(x)≥0在x>2上恒成立,将a分离,在利用基本不等式求出不等式另一侧的最大值,结合(1)可求出a的范围.
解答:解:(1)f'(x)=x2+2ax-b由f'(1)=1⇒b=2a
又由f(x)有极值?△=4a2+4b>0⇒a2+b>0
∴a2+2a>0⇒a<-2或a>0…(4)分
(2)f(x)在x>2上是单增函数
则f'(x)=x2+2ax-2a≥0在x>2上恒成立…(7)分⇒2a(1-x)≤x2 …(9)分
…(9)分
令 t=x-1>1,则只需求 的值域
的值域
当t>1时, ∴
∴
∴a≥-2,又a<-2或a>0故a的取值范围为a>0…(12)分
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及极值问题和利用基本不等式求出最值,属于中档题.
(2)根据f(x)在x>2上是单增函数则f'(x)≥0在x>2上恒成立,将a分离,在利用基本不等式求出不等式另一侧的最大值,结合(1)可求出a的范围.
解答:解:(1)f'(x)=x2+2ax-b由f'(1)=1⇒b=2a
又由f(x)有极值?△=4a2+4b>0⇒a2+b>0
∴a2+2a>0⇒a<-2或a>0…(4)分
(2)f(x)在x>2上是单增函数
则f'(x)=x2+2ax-2a≥0在x>2上恒成立…(7)分⇒2a(1-x)≤x2
 …(9)分
…(9)分令 t=x-1>1,则只需求
 的值域
的值域当t>1时,
 ∴
∴
∴a≥-2,又a<-2或a>0故a的取值范围为a>0…(12)分
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及极值问题和利用基本不等式求出最值,属于中档题.

练习册系列答案
相关题目
 (a,b为实数),且f(lglog310)=5,则f(lglg3)=________.
(a,b为实数),且f(lglog310)=5,则f(lglg3)=________. ,a、b为实数)有极值,且x=1处的切线与直线x-y+1=0平行.
,a、b为实数)有极值,且x=1处的切线与直线x-y+1=0平行.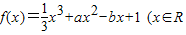 ,a、b为实数)有极值,且x=1处的切线与直线x-y+1=0平行.
,a、b为实数)有极值,且x=1处的切线与直线x-y+1=0平行.