题目内容
已知 (a,b为实数),且f(lglog310)=5,则f(lglg3)=________.
(a,b为实数),且f(lglog310)=5,则f(lglg3)=________.
-3
分析:设lglog310=m,则lglg3=-lg310=-m.令 =h(x)+1,有条件求得f(m)的值,再根据
=h(x)+1,有条件求得f(m)的值,再根据
h(-m)=-h(m),求出f(lglg3)=h(-m)+1的值.
解答:设lglog310=m,则 lglg3=-lglog310=-m.
令 =h(x)+1,则h(x)为奇函数,故h(-m)=-h(m).
=h(x)+1,则h(x)为奇函数,故h(-m)=-h(m).
∵f(lglog310)=f(m)=h(m)+1=5,∴h(m)=4,h(-m)=-4.
∴f(lglg3)=f(m)=h(-m)+1=-4+1=-3,
故答案为-3.
点评:本题主要考查对数的运算性质,函数值的求法,是基础题,解题时要认真审题,仔细解答,属于基础题.
分析:设lglog310=m,则lglg3=-lg310=-m.令
 =h(x)+1,有条件求得f(m)的值,再根据
=h(x)+1,有条件求得f(m)的值,再根据h(-m)=-h(m),求出f(lglg3)=h(-m)+1的值.
解答:设lglog310=m,则 lglg3=-lglog310=-m.
令
 =h(x)+1,则h(x)为奇函数,故h(-m)=-h(m).
=h(x)+1,则h(x)为奇函数,故h(-m)=-h(m).∵f(lglog310)=f(m)=h(m)+1=5,∴h(m)=4,h(-m)=-4.
∴f(lglg3)=f(m)=h(-m)+1=-4+1=-3,
故答案为-3.
点评:本题主要考查对数的运算性质,函数值的求法,是基础题,解题时要认真审题,仔细解答,属于基础题.

练习册系列答案
相关题目
 ,a、b为实数)有极值,且x=1处的切线与直线x-y+1=0平行.
,a、b为实数)有极值,且x=1处的切线与直线x-y+1=0平行.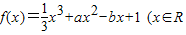 ,a、b为实数)有极值,且x=1处的切线与直线x-y+1=0平行.
,a、b为实数)有极值,且x=1处的切线与直线x-y+1=0平行.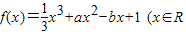 ,a、b为实数)有极值,且x=1处的切线与直线x-y+1=0平行.
,a、b为实数)有极值,且x=1处的切线与直线x-y+1=0平行.