题目内容
19.将半径为R的半圆形铁皮制作成一个无盖圆锥形容器(不计损耗),则其容积为( )| A. | $\frac{{\sqrt{3}}}{24}π{R^3}$ | B. | $\frac{{\sqrt{3}}}{8}π{R^3}$ | C. | $\frac{{\sqrt{5}}}{24}π{R^3}$ | D. | $\frac{{\sqrt{5}}}{8}π{R^3}$ |
分析 推导出设这个盖圆锥形底面半径r=$\frac{R}{2}$,母线长l=R,高h=$\sqrt{{R}^{2}-(\frac{R}{2})^{2}}$=$\frac{\sqrt{3}}{2}R$,由此能求出这个无盖圆锥形容器(不计损耗)的容积.
解答 解:将半径为R的半圆形铁皮制作成一个无盖圆锥形容器,
设这个盖圆锥形底面半径为r,则πR=2πr,解得r=$\frac{R}{2}$,
这个盖圆锥形母线长l=R,
∴这个盖圆锥形的高h=$\sqrt{{R}^{2}-(\frac{R}{2})^{2}}$=$\frac{\sqrt{3}}{2}R$,
∴这个无盖圆锥形容器(不计损耗)的容积:
V=$\frac{1}{3}×S×h$=$\frac{1}{3}×π{r}^{2}×h$
=$\frac{1}{3}×π×(\frac{R}{2})^{2}×\frac{\sqrt{3}}{2}R$
=$\frac{\sqrt{3}}{24}π{R}^{3}$.
故选:A.
点评 本题考查圆锥的容积的求法,考查推理论证能力、运算求解能力,考查等价转化思想、数形结合思想,考查空间思维能力,是中档题.

练习册系列答案
相关题目
10.已知函数f(x)=-x2+ax-b,若a,b都是从[0,4]上任取的一个数,则满足f(1)>0时的概率( )
| A. | $\frac{1}{32}$ | B. | $\frac{9}{32}$ | C. | $\frac{31}{32}$ | D. | $\frac{23}{32}$ |
7.已知集合A={x|x2-3x<0},B={-1,0,1,2,3},则A∩B=( )
| A. | {-1} | B. | {1,2} | C. | {0,3} | D. | {-1,1,2,3} |
4.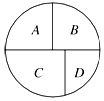 如图所示,用五种不同的颜色分别给A,B,C,D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法共有( )种.
如图所示,用五种不同的颜色分别给A,B,C,D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法共有( )种.
 如图所示,用五种不同的颜色分别给A,B,C,D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法共有( )种.
如图所示,用五种不同的颜色分别给A,B,C,D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法共有( )种.| A. | 120种 | B. | 150 种 | C. | 180 种 | D. | 240 种 |
11.下列函数中,在(0,+∞)内为增函数的是( )
| A. | y=sin x | B. | y=xe2 | C. | y=x3-x | D. | y=ln x-x |
4.下列各组向量互相垂直的是( )
| A. | $\overrightarrow{a}$=(1,2,-2),$\overrightarrow{b}$=(-2,-4,1) | B. | $\overrightarrow{a}$=(2,4,5),$\overrightarrow{b}$=(0,0,0) | ||
| C. | $\overrightarrow{a}$=(1,2,$\frac{1}{2}$),$\overrightarrow{b}$=($\frac{1}{2}$,-$\frac{1}{2}$,1) | D. | $\overrightarrow{a}$=(2,4,5),$\overrightarrow{b}$=(-2,-4,-5) |