题目内容
如图，四棱锥P-ABCD中，PD⊥底面ABCD，PD=DC=2AD,AD⊥DC,∠BCD=45°．
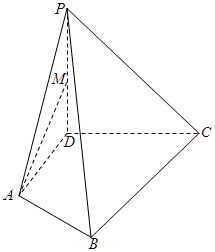
（Ⅰ）设PD的中点为M，求证：AM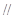
平面PBC；
（Ⅱ）求PA与平面PBC所成角的正切值.
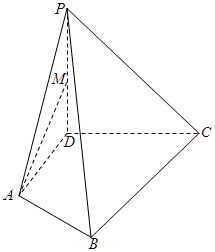
（Ⅰ）设PD的中点为M，求证：AM
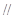平面PBC；（Ⅱ）求PA与平面PBC所成角的正切值.
(I)见解析 （Ⅱ）
（Ⅰ）利用所给直线的向量与已知平面的法向量垂直可证明直线与平面平行；（Ⅱ）利用直线所在的向量与平面法向量的夹角与直线与平面的夹角互余可求出所求角
(I),如图建立空间直角坐标系．
设
,则
，
，
． ……2分
设平面
的一个法向量为
，则
令
得
． ……4分
而
，所以
，即
，又
平面
故
平面．……6分
（Ⅱ）
，设
与平面所成角为
，
由直线与平面所成角的向量公式有
．…11分
(I),如图建立空间直角坐标系．
设
,则，，． ……2分设平面
的一个法向量为，则令
得． ……4分而
，所以，即，又平面故
平面．……6分（Ⅱ）
，设与平面所成角为，由直线与平面所成角的向量公式有
．…11分
练习册系列答案
相关题目
中，
，沿对角线
把
折起到
位置，且
在面
内的射影
恰好落在
上
；
所成的角的正弦值.
，
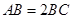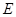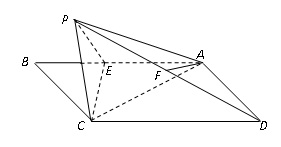
为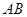
上一点，以直线EC为折线将点B折起至点P，并保持∠PEB为锐角，连结PA、PC、PD，取PD的中点F，若有AF∥平面PEC。
