题目内容
9.如图1,已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=$\frac{π}{2}$,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE=x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF(如图2)
(1)若以F、B、C、D为顶点的三棱锥的体积记为f(x),求f(x)的最大值.
(2)当f(x)取最大值时,是否有BD⊥EG,并说明理由.
分析 (1)由面面垂直性质定理证出AE⊥面EBCF,求出以F、B、C、D为顶点的三棱锥的体积,利用二次函数的图象与性质可得当x=2时,即AE=2时函数有最大值;
(2)作DH⊥EF于H,连BH,GH.由面面垂直性质定理,证出DH⊥平面EBCF,从而得到EG⊥DH.由正方形BGHE中,EG⊥BH且BH∩DH=H,可得EG⊥平面DBH,从而证出BD⊥EG;
解答 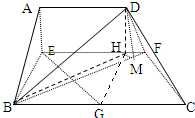 解:(1)∵AE⊥EF,面AEFD⊥面EBCF,面AEFD∩面EBCF=EF
解:(1)∵AE⊥EF,面AEFD⊥面EBCF,面AEFD∩面EBCF=EF
∴AE⊥面EBCF
由题意可得$f(x)=\frac{1}{3}{S}_{△BFC}•AE=\frac{1}{3}×\frac{1}{2}×4•(4-x)•x=\frac{1}{3}(-2{x}^{2}+8x),0<x<4$
所以当$x=2时,f(x)最大为\frac{8}{3}$
(2)证明:作DH⊥EF,交EF于H,连结BH,HG,
因为面AEFD⊥面EBCF,所以DH⊥面BECF.
又EG?面BEFC,所以DH⊥EG,
又x=2时,BE=EH=BG=2.
故四边形BEHG为正方形.
所以BH⊥EG,所以EG⊥面BHD.
又因BD?面BHD,所以BD⊥EG.
点评 本题给出平面图形的翻折问题,在所得几何体中证明线线垂直并求三棱锥体积的最大值,着重考查了空间线面垂直、面面垂直的判定与性质、锥体体积和二次函数的图象与性质等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.曲线y=ax2-ax+1(a≠0)在点(0,1)处的切线与直线3x+y+1=0垂直,则a=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
 如图:PA⊥平面ABCD,ABCD是矩形,PA=AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E边BC上移动.
如图:PA⊥平面ABCD,ABCD是矩形,PA=AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E边BC上移动.