题目内容
【题目】已知向量
，
，角
，
，
为
的内角，其所对的边分别为
，
，
.
（1）当
取得最大值时，求角的大小；
（2）在（1）成立的条件下，当
时，求
的取值范围.
【答案】（1）
（2）
【解析】分析：（1）由两向量的坐标，利用平面向量的数量积运算列出关系式，利用诱导公式及二倍角的余弦函数公式化简，整理后得到关于
的二次函数，由
的范围求出
的范围，利用正弦函数的图象与性质得出此时的范围，利用二次函数的性质即可求出
取得最大值时的度数；
（2）由
及
的值，利用正弦定理表示出
，再利用三角形的内角和定理用
表示出，将表示出的代入
中，利用二倍角的余弦函数公式化简，整理后利用两角和与差的正弦函数公式化为一个角的正弦函数，由的范围求出这个角的范围，利用正弦函数的图象与性质求出此时正弦函数的值域，即可确定出的取值范围．
详解：
（1）
，令
，
，
原式
，当
，即
，时，取得最大值.
（2）当时，
，
.由正弦定理得：
（
为
的外接圆半径）
于是
.
由，得
，于是
，
，
所以的范围是
.
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
【题目】已知产品
的质量采用综合指标值
进行衡量，
为一等品；
为二等品；
为三等品.我市一家工厂准备购进新型设备以提高生产产品的效益，在某供应商提供的设备中任选一个试用，生产了一批产品并统计相关数据，得到频率分布直方图：
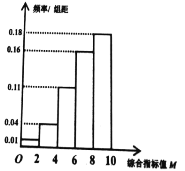
（1）估计该新型设备生产的产品为二等品的概率；
（2）根据这家工厂的记录，产品各等次的销售率（某等次产品销量与其对应产量的比值）及单件售价情况如下：
一等品 | 二等品 | 三等品 | |
销售率 |
|
|
|
单件售价 |
|
|
|
根据以往的销售方案，未售出的产品统一按原售价的
全部处理完.已知该工厂认购该新型设备的前提条件是，该新型设备生产的产品同时满足下列两个条件：
①综合指标值的平均数不小于
（同一组中的数据用该组区间的中点值作代表）；
②单件平均利润值不低于
.
若该新型设备生产的产品的成本为
元/件，月产量为
件，在销售方案不变的情况下，根据以上图表数据，分析该新型设备是否达到该工厂的认购条件.
