Question

正方形ABCD的边AB在直线y=x+4上，C、D两点在抛物线y²=x上，则正方形ABCD的面积为

18或50

．

Answer 1

分析：如图所示，设C(

y

2 1

，y1)，D(

y

2 2

，y2)．利用CD∥AB，可得k_CD=k_AB，再利用正方形ABCD可得|BC|=|CD|，即可解出，进而取得面积．

解答：解：如图所示，设C(

y

2 1

，y1)，D(

y

2 2

，y2)．不妨设y₁＜y₂．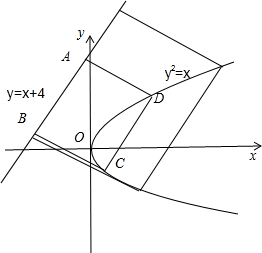
∵CD∥AB，∴k_CD=k_AB，∴

y2-y1

y 2 2 - y 2 1

=1，化为y₁+y₂=1．①
由正方形ABCD可得|BC|=|CD|，∴

| y 2 1 -y1+4|

2

=

( y 2 1 - y 2 2 )2+(y1-y2)2

，②
①②联立化为(

y

2 1

+3y1+2)(

y

2 1

-5y1+6)=0，解得y₁=-1或-2或2或3．
取

y1=-1 y2=2

，

y1=-2 y2=3

．
当取

y1=-1 y2=2

时，|BC|=

|1+1+4|

2

=3

2

，∴正方形ABCD的面积S=(3

2

)2=18．
当取

y1=-2 y2=3

．|BC|=

|4+2+4|

2

=5

2

，∴正方形ABCD的面积S=50．
故答案为18或50．

点评：本题考查了正方形的性质、平行线之间的斜率关系、点到直线的距离公式等基础知识与基本技能方法，属于难题．