题目内容
已知x>0,y>0,xy=x+2y,若xy≥m-2恒成立,则实数m的最大值是 .
10
解析:由x>0,y>0,xy=x+2y≥2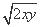 ,
,
得xy≥8,
于是由m-2≤xy恒成立,
得m-2≤8,m≤10,故m的最大值为10.
答案:10

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
已知x>0,y>0,xy=x+2y,若xy≥m-2恒成立,则实数m的最大值是 .
10
解析:由x>0,y>0,xy=x+2y≥2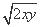 ,
,
得xy≥8,
于是由m-2≤xy恒成立,
得m-2≤8,m≤10,故m的最大值为10.
答案:10

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案