Question

【题目】下列命题:

①关于、的二元一次方程组的系数行列式是该方程组有解的必要非充分条件;

②已知、、、是空间四点,命题甲:、、、四点不共面,命题乙:直线和不相交,则甲成立是乙成立的充分非必要条件;

③“”是“对任意的实数,恒成立”的充要条件;

④“或”是“关于的方程有且仅有一个实根”的充要条件;

其中,真命题序号是________

Answer 1

【答案】②

【解析】

根据充分条件和必要条件的定义逐一判断,即可得出答案.

对于①, 系数行列式,关于、的二元一次方程组有唯一解,

是该方程组有解的非充分条件

又系数行列式,或

关于、的二元一次方程组无解

系数行列式,

关于、的二元一次方程组有无穷组解

关于、的二元一次方程组的系数行列式是该方程组有解的非必要非充分条件;

故①不正确;

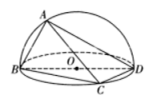
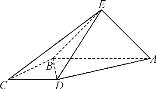
对于②,已知、、、是空间四点,命题甲:、、、四点不共面,命题乙:直线和不相交.

命题甲可以推出命题乙,甲成立是乙成立的充分条件

又直线和不相交,当,即、、、四点共面,

命题乙不能推出命题甲,甲成立是乙成立的非必要条件

甲成立是乙成立的充分非必要条件.

故②正确;

对于③,设

当时,;

当时,;

当时,.

故

能推出任意的实数,

又对任意的实数,不能推出

故“”是“对任意的实数,恒成立”的充分不必要条件

故③不成立;

对于④,由关于的实系数方程有且仅有一个实数根,得:,

由得:或

当时,得,检验知:不是方程的实根,故此时方程无解

当时,,解得,检验知:是方程的实根.

故此时关于的方程有且仅有一个实数根

“或”不能推出“关于的方程有且仅有一个实根”

又关于的方程有且仅有一个实根也不能推出“或”

“或”是“关于的方程有且仅有一个实根”的既不充分也不必要条件.

故④错误.

故答案为:②.