题目内容
【题目】已知函数![]() ,实数
,实数![]() 且
且![]() .
.
(1)设![]() ,判断函数
,判断函数![]() 在
在![]() 上的单调性,并说明理由;
上的单调性,并说明理由;
(2)设![]() 且
且![]() 时,
时,![]() 的定义域和值域都是
的定义域和值域都是![]() ,求
,求![]() 的最大值;
的最大值;
(3)若不等式![]() 对
对![]() 恒成立,求
恒成立,求![]() 的范围.
的范围.
【答案】(1)单调递增,证明见解析;(2)![]() ;(3)
;(3)![]() 且
且![]()
【解析】
(1)根据函数单调性定义作差判断函数单调性;
(2)根据单调性确定![]() ,
,![]() ,再转化为对应方程实根分布问题,根据韦达定理以及求根公式得
,再转化为对应方程实根分布问题,根据韦达定理以及求根公式得![]() 关于
关于![]() 的函数关系式,最后根据二次函数性质求最值得结果;
的函数关系式,最后根据二次函数性质求最值得结果;
(3)先根据绝对值定义化简不等式,变量分离转化为求对应函数最值,
(1)设![]() ,则
,则![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() ,
,
即![]() ,因此函数
,因此函数![]() 在
在![]() 上的单调递增.
上的单调递增.
(2)由(1)及![]() 的定义域和值域都是
的定义域和值域都是![]() 得
得![]() ,
,![]() ,
,
因此![]() ,
,![]() 是方程
是方程![]() 的两个不相等的正数根,
的两个不相等的正数根,
等价于方程![]() 有两个不等的正数根,
有两个不等的正数根,
即![]() 且
且![]() 且
且![]() ,
,
解得![]() ,
,
∴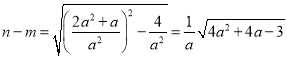
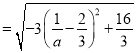 ,
,
∵![]() ,∴
,∴![]() 时,
时,![]() 最大值为
最大值为![]() .
.
(3)![]() ,则不等式
,则不等式![]() 对
对![]() 恒成立,
恒成立,
即![]() ,即不等式
,即不等式![]() 对
对![]() 恒成立,
恒成立,
令![]() ,易证
,易证![]() 在
在![]() 递增,同理
递增,同理![]() 在
在![]() 递减.
递减.
∴![]() ,
,![]() ,
,
∴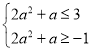 ,∴
,∴![]() 且
且![]() .
.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目