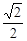题目内容
已知向量
=(sinx+cosx,2),
=(1,sinxcosx),设f(x)=
•
,x∈[0,
],求f(x)的值域.
| a |
| b |
| a |
| b |
| π |
| 2 |
f(x)=
•
=(sinx+cosx,2)•(1,sinxcosx)=sinx+cosx+2sinxconx,
令sinx+cosx=t,∵x∈[0,
],∴t=
sin(x+
)∈[1,
],
则y=t+t2-1=(t+
)2-
则[1,
]上递增,
∴ymin=1,ymax=
+1,
故f(x)的值域为:[1,1+
].
| a |
| b |
令sinx+cosx=t,∵x∈[0,
| π |
| 2 |
| 2 |
| π |
| 4 |
| 2 |
则y=t+t2-1=(t+
| 1 |
| 2 |
| 5 |
| 4 |
| 2 |
∴ymin=1,ymax=
| 2 |
故f(x)的值域为:[1,1+
| 2 |

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
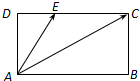
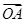 ·
·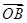 =0,存在实数λ,μ,使得
=0,存在实数λ,μ,使得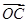 =λ
=λ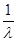 +
+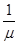 =1
=1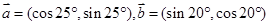 ,若
,若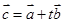 (
(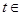
 ),则
),则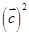 的最小值为( )
的最小值为( )