题目内容
某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成n小块地,在总共2n小块地中,随机选n小块地种植品种甲,另外n小块地种植品种乙.
(1)假设n=4,在第一大块地中,种植品种甲的小块地的数目记为X,求X的分布列和数学期望;
(2)试验时每大块地分成8小块,即n=8,试验结束后得到品种甲和品种乙在各小块地上的每公顷产量(单位:kg/hm2)如下表:
| 品种甲 | 403 | 397 | 390 | 404 | 388 | 400 | 412 | 406 |
| 品种乙 | 419 | 403 | 412 | 418 | 408 | 423 | 400 | 413 |
(1)X的分布列为
2X 0 1 2 3 4 P 




(2)应该选择种植品种乙
解析解:(1)X可能的取值为0,1,2,3,4,
且P(X=0)= =
= ,P(X=1)=
,P(X=1)= =
= ,
,
P(X=2)= =
= ,P(X=3)=
,P(X=3)= =
= ,
,
P(X=4)= =
= .即X的分布列为
.即X的分布列为
X的数学期望是:X 0 1 2 3 4 P 




E(X)=0× +1×
+1× +2×
+2× +3×
+3× +4×
+4× =2.
=2.
(2)品种甲的每公顷产量的样本平均数和样本方差分别为: 甲=
甲= (403+397+390+404+388+400+412+406)=400,
(403+397+390+404+388+400+412+406)=400,
S2甲= (32+(-3)2+(-10)2+42+(-12)2+02+122+62)=57.25.
(32+(-3)2+(-10)2+42+(-12)2+02+122+62)=57.25.
品种乙的每公顷产量的样本平均数和样本方差分别为: 乙=
乙= (419+403+412+418+408+423+400+413)=412,
(419+403+412+418+408+423+400+413)=412,
S2乙= (72+(-9)2+02+62+(-4)2+112+(-12)2+12)=56.
(72+(-9)2+02+62+(-4)2+112+(-12)2+12)=56.
由以上结果可以看出,品种乙的样本平均数大于品种甲的样本平均数,且两品种的样本方差差异不大,故应该选择种植品种乙.

为了解心肺疾病是否与年龄相关,现随机抽取了40名市民,得到数据如下表:
| | 患心肺疾病 | 不患心肺疾病 | 合计 |
| 大于40岁 | 16 | | |
| 小于等于40岁 | | 12 | |
| 合计 | | | 40 |
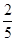
(1)请将
 列联表补充完整;
列联表补充完整;(2)已知大于40岁患心肺疾病市民中,经检查其中有4名重症患者,专家建议重症患者住院治疗,现从这16名患者中选出两名,记需住院治疗的人数为
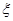 ,求
,求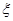 的分布列和数学期望;
的分布列和数学期望;(3)能否在犯错误的概率不超过0.01的前提下认为患心肺疾病与年龄有关?
下面的临界值表供参考:
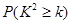 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
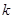 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
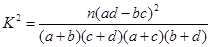 ,其中
,其中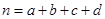 )
) 甲、乙两药厂生产同一型号药品,在某次质量检测中,两厂各有5份样品送检,检测的平均得分相等(检测满分为100分,得分高低反映该样品综合质量的高低).成绩统计用茎叶图表示如下:
| 甲 | | 乙 |
| 9 8 | 8 | 4 8 9 |
| 2 1 0 | 9 |  6 6 |
(1)求
 ;
;(2)某医院计划采购一批该型号药品,从质量的稳定性角度考虑,你认为采购哪个药厂的产品
比较合适?
(3)检测单位从甲厂送检的样品中任取两份作进一步分析,在抽取的两份样品中,求至少有一份得分在(90,100]之间的概率.
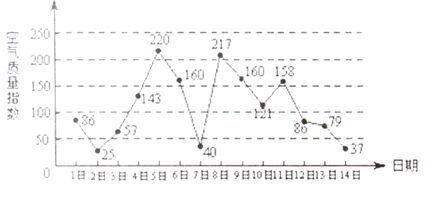
 ,
,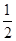 ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为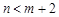 的概率.
的概率.