题目内容

1．变量x，y满足约束条件$\left\{\begin{array}{l}{x+4y-13≥0}\\{2y-x+1≥0}\\{x+y-4≤0}\end{array}\right.$，且有无穷多个点（x，y）使目标函数z=x+my取得最小值，则m=（　　）
A．-2B．-1C．1D．4

分析 先画出可行域，再研究目标函数，由于目标函数中含有参数m，故需讨论m的正负，再结合可行域，将目标函数赋予几何意义，数形结合确定满足题意的m的值

解答 解：画出可行域如图阴影区域：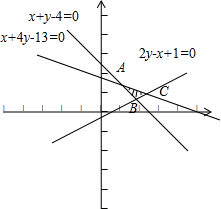
若m=0，则z=x，目标函数z=x+my取得最小值的最优解只有一个，不合题意
若m≠0，目标函数z=x+my可看做斜率为-$\frac{1}{m}$的动直线y=-$\frac{1}{m}$x+$\frac{z}{m}$
若m＜0，则-$\frac{1}{m}$＞0，数形结合知使目标函数z=x+my取得最小值的最优解不可能有无穷多个，
若m＞0，则-$\frac{1}{m}$＜0，数形结合可知，当动直线与直线AB平行时有无穷多个点（x，y）在线段AB上，使目标函数z=x+my取得最小值，
即-$\frac{1}{m}$=-1，m=1
故选：C．

点评 本题主要考查了线性规划的思想及其应用，可行域的画法及其应用，目标函数的意义，数形结合转化化归的思想方法，属中档题

练习册系列答案
相关题目
10．设二次函数f（x）满足：对任意x∈R，都有f（x+1）+f（x）=2x2-2x-3
（1）求f（x）的解析式；
（2）若关于x的方程f（x）=a有两个实数根x1，x2，且满足：-1＜x1＜2＜x2，求实数a的取值范围．
12．设f（x）=4sin（2x-$\frac{π}{3}$）+$\sqrt{3}$．
（1）求f（x）在[0，$\frac{π}{2}$]上的最大值和最小值；
（2）把y=f（x）的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再把得到的图象向左平移$\frac{2π}{3}$个单位，得到函数y=g（x）的图象，求g（x）的单调减区间．
9．某同学寒假期间对其30位亲属的饮食习惯进行了一次调查，列出了如表2×2列联表：
偏爱蔬菜偏爱肉类合计
50岁以下4812
50岁以上16218
合计201030
则可以说其亲属的饮食习惯与年龄有关的把握为（　　）
附：参考公式和临界值表K2=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$
P（K2≥k）0.0500.0100.001
k3.8416.63510.828
A．90%B．95%C．99%D．99.9%
16．给定下列三个命题：
p1：若p∧q为假命题，则p，q均为假命题
p2：?a，b∈R，a2-ab+b2＜0；
p3：在三角形ABC中，A＞B，则sinA＞sinB．
则下列命题中的真命题为（　　）
A．p1∨p2B．p2∧p3C．p1∨（￢p3）D．（￢p2）∧p3
6．已知偶函数f（x）在[0，+∞）上单调递减，若f（x-2）＞f（3），则x的取值范围是[-1，5]．
13．已知圆O：x2+y2=1，圆M：（x-a）2+（y-$\sqrt{3}$a）2=1．若圆M上存在点P，过点P作圆O的两条切线，切点为A，B，使得∠APB=60°，则实数a的取值范围为$[{\frac{1}{2}，\frac{3}{2}}]∪[{-\frac{3}{2}，-\frac{1}{2}}]$．
10．当a=3时，如图的程序框图输出的结果是（　　）
A．9B．3C．10D．6
11．已知函数f（x）=$\left\{\begin{array}{l}{（1-2a）x+5，（x≤12）}\\{{a}^{x-13}，（x＞12）}\end{array}\right.$，若数列{an}满足an=f（n）（n∈N*），且对任意的两个正整数m，n（m≠n）都有（m-n）（am-an）＜0，则实数a的取值范围是（　　）
A．（$\frac{1}{2}$，$\frac{2}{3}$]B．（$\frac{1}{2}$，$\frac{3}{4}$）C．（$\frac{3}{4}$，1）D．（$\frac{1}{2}$，$\frac{2}{3}$）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网