题目内容
已知圆G: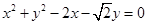 经过椭圆
经过椭圆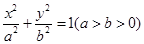 的右焦点F及上顶点B,过椭圆外一点(m,0)(
的右焦点F及上顶点B,过椭圆外一点(m,0)( )倾斜角为
)倾斜角为 的直线L交椭圆与C、D两点.
的直线L交椭圆与C、D两点.
(1)求椭圆的方程;
(2)若右焦点F在以线段CD为直径的圆E的内部,求m的取值范围.
(1)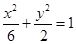 ;(2)
;(2)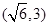 .
.
解析试题分析:
解题思路:(1)求出圆与两坐标轴的交点,即得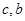 的值,进而求得椭圆方程;(2)联立直线与椭圆的方程,整理成关于
的值,进而求得椭圆方程;(2)联立直线与椭圆的方程,整理成关于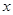 的一元二次方程,再利用
的一元二次方程,再利用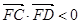 求解.
求解.
规律总结:圆锥曲线的问题一般都有这样的特点:第一小题是基本的求方程问题,一般简单的利用定义和性质即可;后面几个小题一般来说综合性较强,用到的内容较多,大多数需要整体把握问题并且一般来说计算量很大,学生遇到这种问题就很棘手,有放弃的想法,所以处理这类问题一定要有耐心.
试题解析:(1) 圆
圆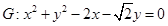 经过点F、B,
经过点F、B,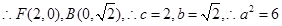 故椭圆的方程为
故椭圆的方程为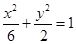 ;
;
(2)设直线L的方程为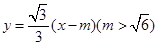
由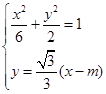 消去
消去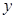 得
得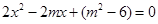
由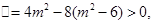 解得
解得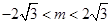 。
。
又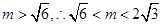
设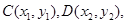 则
则 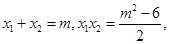
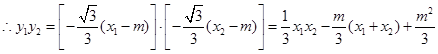
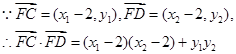

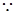 点F在圆E内部,
点F在圆E内部,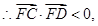 即
即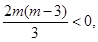 解得0<m<3
解得0<m<3
∴m的取值范围是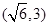 .
.
考点:1.圆的标准方程;2.直线与椭圆的位置关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的焦点为F2,点F1与F2关于坐标原点对称,直线m垂直于x轴(垂足为T),与抛物线交于不同的两点P,Q且
的焦点为F2,点F1与F2关于坐标原点对称,直线m垂直于x轴(垂足为T),与抛物线交于不同的两点P,Q且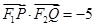 .
.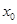 ;
;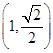 .
.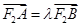 ,若
,若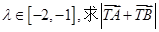 的取值范围.
的取值范围.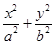 =1(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.
=1(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.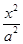 +
+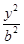 =1(a>b>0)过点(0,4),离心率为
=1(a>b>0)过点(0,4),离心率为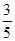 .
.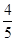 的直线被C所截线段的中点坐标.
的直线被C所截线段的中点坐标.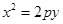 的焦点为F,
的焦点为F,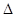 ABQ的三个顶点都在抛物线C上,点M为AB的中点,
ABQ的三个顶点都在抛物线C上,点M为AB的中点,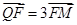 .(1)若M
.(1)若M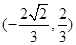 ,求抛物线C方程;(2)若
,求抛物线C方程;(2)若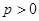 的常数,试求线段
的常数,试求线段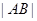 长的最大值.
长的最大值.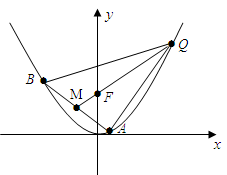
 的左,右两个顶点分别为
的左,右两个顶点分别为 、
、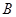 .曲线
.曲线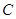 是以
是以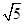 的双曲线.设点
的双曲线.设点 在第一象限且在曲线
在第一象限且在曲线 与椭圆相交于另一点
与椭圆相交于另一点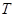 .
.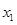 ,
,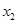 ,证明:
,证明: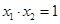 .
.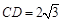 ,
,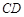 的中点为
的中点为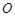 ,动点
,动点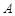 满足
满足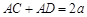 (
(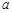 为正常数).
为正常数).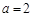 ,动点
,动点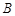 满足
满足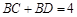 ,且
,且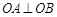 ,试求
,试求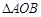 面积的最大值和最小值.
面积的最大值和最小值. 中心在原点,右焦点与抛物线
中心在原点,右焦点与抛物线 的焦点重合,则该双曲线的离心率为___________
的焦点重合,则该双曲线的离心率为___________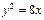 的准线与x轴交于点Q,若过点Q的直线
的准线与x轴交于点Q,若过点Q的直线 与抛物线有公共点,则直线
与抛物线有公共点,则直线