题目内容
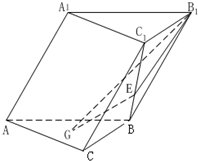 如图,在斜三棱柱ABC-A1B1C1 中,侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成600的角,AA1=2.底面ABC是边长为2的正三角形,其重心为G点.E是线段BC1上一点,且BE=
如图,在斜三棱柱ABC-A1B1C1 中,侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成600的角,AA1=2.底面ABC是边长为2的正三角形,其重心为G点.E是线段BC1上一点,且BE=| 1 | 3 |
(1)求证:GE∥侧面AA1B1B;
(2)求平面B1GE与底面ABC所成锐二面角的大小.
分析:(1)要证明GE∥侧面AA1B1B,可在平面AA1B1B内找到一条与EG平行的直线,根据G为底面三角形的重心,而E点满足
BE=
BC1,延长B1E交BC于一点F,利用三角形相似得到F为BC的中点,说明A、G、F三点共线,连结GE,根据平行线截线段成比例定理得到GE∥AB1,从而得到要证的结论;
(2)根据侧面AA1B1B⊥底面ABC,直接过B1作B1H⊥AB的延长线于H,垂足为H,然后过H作HT⊥AF的延长线于T,垂足为T,连B1T,由此得到∠B1TH为所求二面角的平面角,然后通过解直角三角形求二面角的大小.
BE=
| 1 |
| 3 |
(2)根据侧面AA1B1B⊥底面ABC,直接过B1作B1H⊥AB的延长线于H,垂足为H,然后过H作HT⊥AF的延长线于T,垂足为T,连B1T,由此得到∠B1TH为所求二面角的平面角,然后通过解直角三角形求二面角的大小.
解答: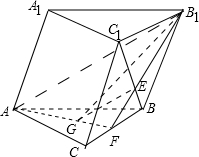 (1)证明:如图,
(1)证明:如图,
连结B1E并延长延长B1E交BC于F,∵△B1EC1∽△FEB,BE=
EC1
∴BF=
B1C1=
BC,从而F为BC的中点.
∵G为△ABC的重心,∴A、G、F三点共线,且
=
=
,∴GE∥AB1,
又GE?侧面AA1B1B,∴GE∥侧面AA1B1B
(2)解:如图,
在侧面AA1B1B内,过B1作B1H⊥AB的延长线于H,垂足为H,∵侧面AA1B1B⊥底面ABC,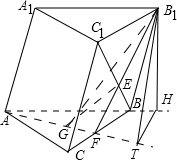
∴B1H⊥底面ABC.又侧棱AA1与底面ABC成600的角,AA1=2,
∴∠B1BH=60°,BH=1,B1H=
.
在底面ABC内,过H作HT⊥AF的延长线于T,垂足为T,连B1T.由三垂线定理有B1T⊥AF,
又平面B1GE与底面ABC的交线为AF,∴∠B1TH为所求二面角的平面角.
∴AH=AB+BH=3,∠HAT=30°,∴HT=AHsin30°=
,
在Rt△B1HT中,tan∠B1TH=
=
,
从而平面B1GE与底面ABC所成锐二面角的大小为arctan
.
 (1)证明:如图,
(1)证明:如图,连结B1E并延长延长B1E交BC于F,∵△B1EC1∽△FEB,BE=
| 1 |
| 2 |
∴BF=
| 1 |
| 2 |
| 1 |
| 2 |
∵G为△ABC的重心,∴A、G、F三点共线,且
| FG |
| FA |
| FE |
| FB1 |
| 1 |
| 3 |
又GE?侧面AA1B1B,∴GE∥侧面AA1B1B
(2)解:如图,
在侧面AA1B1B内,过B1作B1H⊥AB的延长线于H,垂足为H,∵侧面AA1B1B⊥底面ABC,

∴B1H⊥底面ABC.又侧棱AA1与底面ABC成600的角,AA1=2,
∴∠B1BH=60°,BH=1,B1H=
| 3 |
在底面ABC内,过H作HT⊥AF的延长线于T,垂足为T,连B1T.由三垂线定理有B1T⊥AF,
又平面B1GE与底面ABC的交线为AF,∴∠B1TH为所求二面角的平面角.
∴AH=AB+BH=3,∠HAT=30°,∴HT=AHsin30°=
| 3 |
| 2 |
在Rt△B1HT中,tan∠B1TH=
| B1H |
| HT |
2
| ||
| 3 |
从而平面B1GE与底面ABC所成锐二面角的大小为arctan
2
| ||
| 3 |
点评:本题考查了直线与平面平行的判定,考查了二面角的平面角的求法,综合考查了学生的空间想象能力和思维能力,利用三角形的中位线平行于底边及利用平行线截线段成比例定理是证明线面平行常用的方法,此题是中档题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 如图,在斜三棱柱ABC-A1B1C1中,∠A1AB=∠A1AC,AB=AC,A1A=A1B=a,侧面B1BCC1与底面ABC所成的二面角为120°,E、F分别是棱B1C1、A1A的中点
如图,在斜三棱柱ABC-A1B1C1中,∠A1AB=∠A1AC,AB=AC,A1A=A1B=a,侧面B1BCC1与底面ABC所成的二面角为120°,E、F分别是棱B1C1、A1A的中点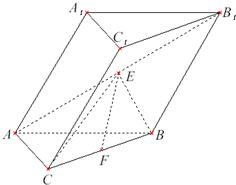 如图,在斜三棱柱ABC-A1B1C1中,AC=BC,AC⊥BC.侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E,F分别是AB1,BC的中点.
如图,在斜三棱柱ABC-A1B1C1中,AC=BC,AC⊥BC.侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E,F分别是AB1,BC的中点.  如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,又BC1⊥AC,过C1作C1H⊥底面ABC,垂足为H,则点H一定在( )
如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,又BC1⊥AC,过C1作C1H⊥底面ABC,垂足为H,则点H一定在( ) (2007•武汉模拟)如图,在斜三棱柱ABC-A1B1C1中 AB=BC=2,∠ABC=120°,又顶点A1在底面ABC上的射影落在AC上,侧棱AA1与底面成60°的角,D为AC的中点.
(2007•武汉模拟)如图,在斜三棱柱ABC-A1B1C1中 AB=BC=2,∠ABC=120°,又顶点A1在底面ABC上的射影落在AC上,侧棱AA1与底面成60°的角,D为AC的中点. (2008•武汉模拟)如图,在斜三棱柱ABC-A'B'C'中,∠ABC=90°,则侧面A'ACC'⊥侧面ABC,又AA'和底面所成60°的角,且AA'=2a,AB=BC=
(2008•武汉模拟)如图,在斜三棱柱ABC-A'B'C'中,∠ABC=90°,则侧面A'ACC'⊥侧面ABC,又AA'和底面所成60°的角,且AA'=2a,AB=BC=