题目内容
已知函数f(x)=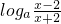 的定义域为[α,β],值域为[logaa(β-1),logaa(α-1)],并且f(x)在[α,β]上为减函数.
的定义域为[α,β],值域为[logaa(β-1),logaa(α-1)],并且f(x)在[α,β]上为减函数.
(1)求a的取值范围;
(2)求证:2<α<4<β;
(3)若函数g(x)=logaa(x-1)-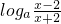 ,x∈[α,β]的最大值为M,求证:0<M<1.
,x∈[α,β]的最大值为M,求证:0<M<1.
解.(1)按题意,得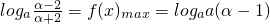 .
.
∴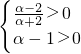 即 α>2. (3分)
即 α>2. (3分)
又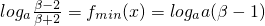
∴关于x的方程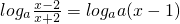 .
.
在(2,+∞)内有二不等实根x=α、β.
?关于x的二次方程ax2+(a-1)x+2(1-a)=0在(2,+∞)内有二异根α、β.
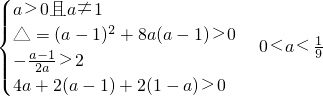 .
.
故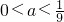 . (6分)
. (6分)
(2)令Φ(x)=ax2+(a-1)x+2(1-a),
则Φ(2)•Φ(4)=4a•(18a-2)=8a(9a-1)<0.
∴2<α<4<β. (10分)
(3)∵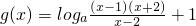 ,
,
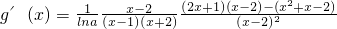
=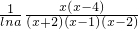 .
.
∵lna<0,
∴当x∈(α,4)时,g'(x)>0;
当x∈(4,β)是g'(x)>0.
又g(x)在[α,β]上连接,
∴g(x)在[α,4]上递增,在[4,β]上递减.
故 M=g(4)=loga9+1=loga9a. (12分)
∵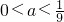 ,
,
∴0<9a<1.
故M>0.
若M≥1,则9a=aM.
∴9=aM-1≤1,矛盾.
故0<M<1. (15分)
分析:(1)由已知中f(x)在[α,β]上为减函数函数f(x)=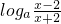 的定义域为[α,β],值域为[logaa(β-1),logaa(α-1)],我们可得
的定义域为[α,β],值域为[logaa(β-1),logaa(α-1)],我们可得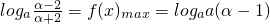 ,根据对数式中底数及真数的限制条件,可得α>2,同理β>2,故关于x的方程
,根据对数式中底数及真数的限制条件,可得α>2,同理β>2,故关于x的方程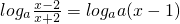 在(2,+∞)内有二不等实根α、β.由此构造关于a的不等式组,解不等式组即可求出a的取值范围;
在(2,+∞)内有二不等实根α、β.由此构造关于a的不等式组,解不等式组即可求出a的取值范围;
(2)令Φ(x)=ax2+(a-1)x+2(1-a),我们易得Φ(2)•Φ(4)<0,进而根据零点存在定理,结合(1)中的结论,得到答案;
(3)由已知中函数g(x)=logaa(x-1)-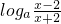 ,x∈[α,β]的解析式,我们利用导数法,可以判断出函数的单调性,进而得到M=g(4)=loga9+1,结合(1)中a的取值范围,即可得到答案.
,x∈[α,β]的解析式,我们利用导数法,可以判断出函数的单调性,进而得到M=g(4)=loga9+1,结合(1)中a的取值范围,即可得到答案.
点评:本题考查的知识点是利用导数研究函数的单调性,导数的运算,利用导数求闭区间上函数的最值,其中(1)的关键是根据函数的单调性将问题转化为关于x的方程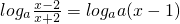 在(2,+∞)内有二不等实根α、β.并由此构造关于a的不等式组,(2)的关键是构造函数Φ(x)=ax2+(a-1)x+2(1-a),将问题转化为函数零点判断问题,(3)的关键是利用导数法,判断出M=g(4).
在(2,+∞)内有二不等实根α、β.并由此构造关于a的不等式组,(2)的关键是构造函数Φ(x)=ax2+(a-1)x+2(1-a),将问题转化为函数零点判断问题,(3)的关键是利用导数法,判断出M=g(4).
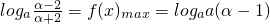 .
.∴
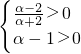 即 α>2. (3分)
即 α>2. (3分)又
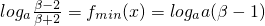
∴关于x的方程
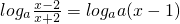 .
.在(2,+∞)内有二不等实根x=α、β.
?关于x的二次方程ax2+(a-1)x+2(1-a)=0在(2,+∞)内有二异根α、β.
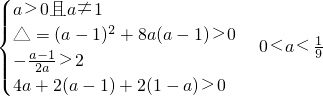 .
. 故
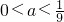 . (6分)
. (6分)(2)令Φ(x)=ax2+(a-1)x+2(1-a),
则Φ(2)•Φ(4)=4a•(18a-2)=8a(9a-1)<0.
∴2<α<4<β. (10分)
(3)∵
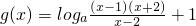 ,
,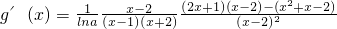
=
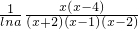 .
.∵lna<0,
∴当x∈(α,4)时,g'(x)>0;
当x∈(4,β)是g'(x)>0.
又g(x)在[α,β]上连接,
∴g(x)在[α,4]上递增,在[4,β]上递减.
故 M=g(4)=loga9+1=loga9a. (12分)
∵
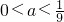 ,
,∴0<9a<1.
故M>0.
若M≥1,则9a=aM.
∴9=aM-1≤1,矛盾.
故0<M<1. (15分)
分析:(1)由已知中f(x)在[α,β]上为减函数函数f(x)=
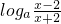 的定义域为[α,β],值域为[logaa(β-1),logaa(α-1)],我们可得
的定义域为[α,β],值域为[logaa(β-1),logaa(α-1)],我们可得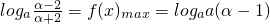 ,根据对数式中底数及真数的限制条件,可得α>2,同理β>2,故关于x的方程
,根据对数式中底数及真数的限制条件,可得α>2,同理β>2,故关于x的方程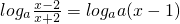 在(2,+∞)内有二不等实根α、β.由此构造关于a的不等式组,解不等式组即可求出a的取值范围;
在(2,+∞)内有二不等实根α、β.由此构造关于a的不等式组,解不等式组即可求出a的取值范围;(2)令Φ(x)=ax2+(a-1)x+2(1-a),我们易得Φ(2)•Φ(4)<0,进而根据零点存在定理,结合(1)中的结论,得到答案;
(3)由已知中函数g(x)=logaa(x-1)-
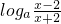 ,x∈[α,β]的解析式,我们利用导数法,可以判断出函数的单调性,进而得到M=g(4)=loga9+1,结合(1)中a的取值范围,即可得到答案.
,x∈[α,β]的解析式,我们利用导数法,可以判断出函数的单调性,进而得到M=g(4)=loga9+1,结合(1)中a的取值范围,即可得到答案.点评:本题考查的知识点是利用导数研究函数的单调性,导数的运算,利用导数求闭区间上函数的最值,其中(1)的关键是根据函数的单调性将问题转化为关于x的方程
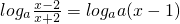 在(2,+∞)内有二不等实根α、β.并由此构造关于a的不等式组,(2)的关键是构造函数Φ(x)=ax2+(a-1)x+2(1-a),将问题转化为函数零点判断问题,(3)的关键是利用导数法,判断出M=g(4).
在(2,+∞)内有二不等实根α、β.并由此构造关于a的不等式组,(2)的关键是构造函数Φ(x)=ax2+(a-1)x+2(1-a),将问题转化为函数零点判断问题,(3)的关键是利用导数法,判断出M=g(4). 
练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
已知函数f(x)=x3的切线的斜率等于1,则这样的切线有( )
| A、1条 | B、2条 | C、3条 | D、不确定 |