题目内容
【题目】数列
，
满足下列条件：①
，
；②当
时，
满足：
时，
，
；
时，
，
.
（1）若
，
，求
和
的值，并猜想数列
可能的通项公式（不需证明）；
（2）若，
，
是满足
的最大整数，求的值.
【答案】（1）见解析；（2）11.
【解析】
（1）利用题中的条件，分别令
，求出
和
的值，并计算
，
，
，
，根据这四项，猜想数列
可能的通项公式；
（2）用反证法说明
时，
，由此推出
，从而得到
通项公式，写出时
通项公式，再由
是满足
的最大整数，得到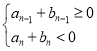
，解之可得整数
.
（1）
，
，故
，
∴
，
，
，
，
，
，
，
，
∴
，，
，
，
故
，
，
，
猜想：
.
（2）
，
，
，
当时，假设存在
使得
，
则有
，与“是满足的最大整数”矛盾，
假设不成立，
时，恒有，
，
，
，，
是以
为首项，
为公比的等比数列，
，，
∵，，
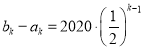时，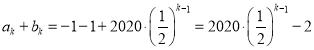
，
，，
时，
，
时，
是单调递减数列，
是满足的最大整数，
时，恒成立；
时，，，
，
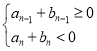即
，
解得
，
为正整数，
，
.
练习册系列答案
阅读快车系列答案
相关题目
