题目内容
已知f(x)是R上的增函数,且(k·3x)-f(9x-3x+2)<0对任意的x∈R都成立,求实数k的取值范围.
解:由已知f(k·3x)<f(9x-3x+2)对任意x∈R恒成立.
y=f(x)在R上是增函数,∴只要k·3x<9x-3x+2恒成立.
令3x=t(t>0),上式等价于g(t)=t2-(k+1)t+2>0对t>0恒成立,由二次函数的图象和性质有
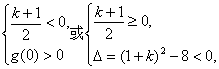
即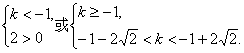
∴k<2![]() -1.
-1.

练习册系列答案
相关题目
题目内容
已知f(x)是R上的增函数,且(k·3x)-f(9x-3x+2)<0对任意的x∈R都成立,求实数k的取值范围.
解:由已知f(k·3x)<f(9x-3x+2)对任意x∈R恒成立.
y=f(x)在R上是增函数,∴只要k·3x<9x-3x+2恒成立.
令3x=t(t>0),上式等价于g(t)=t2-(k+1)t+2>0对t>0恒成立,由二次函数的图象和性质有
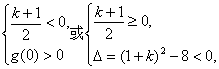
即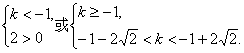
∴k<2![]() -1.
-1.
