Question

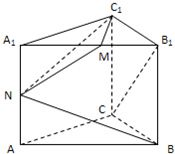
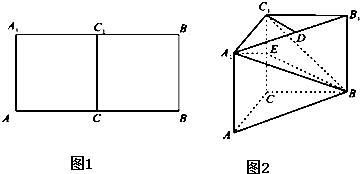
如图，三棱柱ABC-A₁B₁C₁中，侧棱垂直底面，AC⊥BC，D是棱AA₁的中点，AA₁=2AC=2BC=2a（a＞0）．
（1）证明：C₁D⊥平面BDC；
（2）求三棱锥C-BC₁D的体积．

Answer 1

（1）证明：∵BC⊥CC₁，BC⊥AC，AC∩CC₁=C，∴BC⊥平面ACC₁A₁，
C₁D?平面ACC₁A₁，∴BC⊥C₁D，
A₁C₁=A₁D=AD=AC，∴∠A1DC1=∠ADC=

π

4

，
∴∠C1DC=

π

2

，即C₁D⊥DC，
又BD∩CD=C，∴C₁D⊥平面BDC，
（2）三棱锥C-BC₁D即三棱锥C₁-BCD，由（1）知BC⊥CD，
CD=

2

a，BC=a
∴△BCD的面积S=

1

2

×BC×CD=

2

2

a2，
由（1）知，C₁D是三棱锥C₁-BCD底面BDC上的高，
∴体积V=

1

3

Sh=

1

3

×S×C1D=

1

3

×

2

2

a2×

2

a=

1

3

a3．