题目内容
动圆 经过点
经过点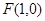 并且与直线
并且与直线 相切,若动圆
相切,若动圆 与直线
与直线 总有公共点,则圆
总有公共点,则圆 的面积( )
的面积( )
A.有最大值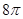 | B.有最小值 | C.有最小值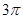 | D.有最小值 |

解析试题分析:设动圆圆心 ,半径为
,半径为 ,依题意则有
,依题意则有 ①,
①, ②,
②, ③,由①②得
③,由①②得 ,代入③得
,代入③得 ,即
,即 ,所以
,所以 ,因此圆
,因此圆 的面积有最小值
的面积有最小值 ,故选择
,故选择 .
.
考点:

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
若圆C: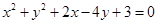 关于直线
关于直线 对称,则由点
对称,则由点 向圆所作的切线长的最小值是( )
向圆所作的切线长的最小值是( )
| A.2 | B.4 | C.3 | D.6 |
已知圆C1:(x-2)2+(y-3)2=1,圆C2:(x-3)2+(y-4)2=9,M,N分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为( )
A.5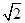 -4 -4 | B.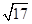 -1 -1 | C.6-2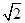 | D.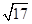 |
若圆的方程为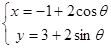 (
( 为参数),直线的方程为
为参数),直线的方程为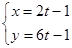 (t为参数),
(t为参数),
则直线与圆的位置关系是( )
| A.相交过圆心 | B.相交而不过圆心 | C.相切 | D.相离 |
过原点且倾斜角为 的直线被圆学
的直线被圆学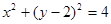 所截得的弦长为(科网 )
所截得的弦长为(科网 )
A.2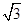 | B.2 | C.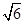 | D.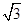 |
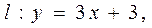
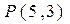 关于直线
关于直线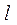 的对称点
的对称点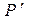 的坐标;
的坐标;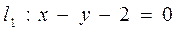 关于直线
关于直线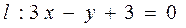 的对称直线
的对称直线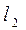 的方程。
的方程。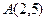 ,
,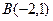 ,
,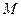 (在第一象限)和
(在第一象限)和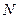 是过原点的直线
是过原点的直线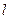 上的两个动点,且
上的两个动点,且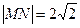 ,
,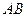 ,如果直线
,如果直线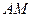 和
和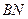 的交点
的交点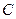 在
在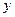 轴上,求点
轴上,求点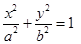
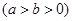 的一个焦点为
的一个焦点为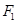 ,若椭圆上存在一个点
,若椭圆上存在一个点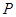 ,满足以椭圆短轴为直径的圆与线段
,满足以椭圆短轴为直径的圆与线段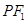 相切于该线段的中点,则椭圆的离心率为( )
相切于该线段的中点,则椭圆的离心率为( ) 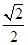
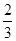
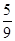
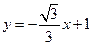 和
和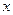 轴,
轴,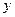 轴分别交于点
轴分别交于点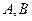 ,以线段
,以线段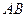 为边在第一象限内作等边△
为边在第一象限内作等边△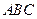 ,如果在第一象限内有一点
,如果在第一象限内有一点 使得△
使得△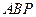 和△
和△ 的值。
的值。