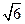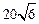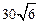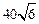题目内容
椭圆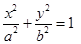
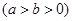 的一个焦点为
的一个焦点为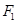 ,若椭圆上存在一个点
,若椭圆上存在一个点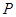 ,满足以椭圆短轴为直径的圆与线段
,满足以椭圆短轴为直径的圆与线段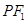 相切于该线段的中点,则椭圆的离心率为( )
相切于该线段的中点,则椭圆的离心率为( )
A.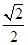 | B.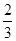 | C.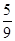 | D.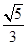 |
D
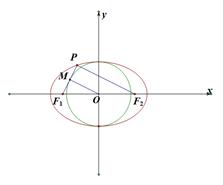
解析试题分析:画出如下示意图.可知0M为△PF1F2的中位线,∴PF2=2OM=2b,∴PF1=2a-PF2=2a-2b,又∵M为PF1的中点,∴MF1=a-b,∴在Rt△OMF1中,由OM2+MF12=OF12,可得(a-b)2+b2=c2=a2-b2.可得2a=3b,进而可得离心率e= .
.
考点:椭圆与圆综合问题.

练习册系列答案
相关题目
动圆 经过点
经过点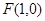 并且与直线
并且与直线 相切,若动圆
相切,若动圆 与直线
与直线 总有公共点,则圆
总有公共点,则圆 的面积( )
的面积( )
A.有最大值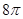 | B.有最小值 | C.有最小值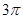 | D.有最小值 |
已知圆 截直线
截直线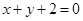 所得弦的长度为4,则实数
所得弦的长度为4,则实数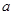 的值为( )
的值为( )
A.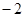 | B.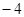 | C.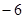 | D.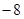 |
圆C:(x+1)2+(y-3)2=9上有两点P,Q关于直线x+my+4=0对称,则m等于( )
A.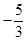 | B.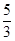 | C.-1 | D.1 |
过点A(-1,0),斜率为k的直线,被圆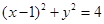 截得的弦长为2
截得的弦长为2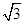 ,则k的值为( )。
,则k的值为( )。
A.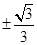 | B. | C.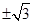 | D.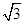 |
圆: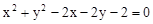 上的点到直线
上的点到直线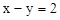 的距离最小值是( ).
的距离最小值是( ).
| A.0 | B.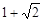 | C.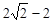 | D. |
直线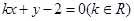 与圆
与圆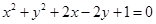 的位置关系是
的位置关系是
| A.相交 | B.相切 | C.相离 | D.与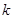 值有关 值有关 |
已知圆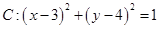 和两点
和两点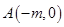 ,
,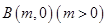 ,若圆
,若圆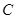 上存在点
上存在点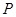 ,使得
,使得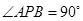 ,则
,则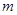 的最大值为( )
的最大值为( )
A. | B. | C.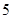 | D.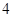 |