题目内容
已知点A,B的坐标分别是(0,–1),(0,1),直线AM,BM相交于点M,且它们的斜率之积为![]() .
.
(1) 求点M的轨迹C的方程;
(2) 过D(2,0)的直线l与轨迹C有两不同的交点时,求l的斜率的取值范围;
(3) 若过点D(2,0)的直线l与(1)中的轨迹C交于不同的两点E、F(E在D、F之间),试求![]() 与
与![]() 面积之比的取值范围(O为坐标原点).
面积之比的取值范围(O为坐标原点).
解:(1) 设点![]() 的坐标为
的坐标为![]() ,
,
∵![]() ,∴
,∴![]() . ……2分
. ……2分
整理,得![]() (
(![]() ),这就是动点M的轨迹方程.············· 4分
),这就是动点M的轨迹方程.············· 4分
(2) 由题意知直线![]() 的斜率存在,设
的斜率存在,设![]() 的方程为
的方程为![]() (
(![]() ) ①
) ①
将①代入![]() ,得
,得![]() (*)
(*)
由![]() ,解得
,解得![]() .····························· 8分
.····························· 8分
(3) 由(*)式得
设![]() ,
,![]() ,则
,则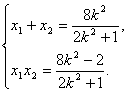 ② ……9分
② ……9分
令![]() ,则
,则![]() ,即
,即![]() ,
,
即![]() ,
,
且![]() ………………………………10分
………………………………10分
由②得,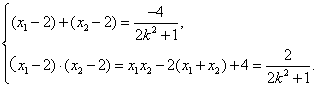
即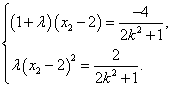
![]() . …………12分
. …………12分
![]() 且
且![]()
![]() 且
且![]() .
.
解得![]() 且
且![]()
![]() ,
,![]() 且
且![]() .
.
∴△OBE与△OBF面积之比的取值范围是![]() .···················· 14分
.···················· 14分

练习册系列答案
相关题目