题目内容
（2012•许昌一模）设向量
，
均为非零向量，（
+2
）⊥
，（
+2
）⊥
，则
，
的夹角为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
分析：由已知（
+2
）⊥
，（
+2
）⊥
，可得（
+2
）•
=0，（
+2
）•
=0，进而根据向量的夹角公式可求答案．
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
解答：解：∵（
+2
）⊥
，（
+2
）⊥
，
∴（
+2
）•
=0，（
+2
）•
=0，
即
•
=-
2=-
2，
∴cosθ=
=-
∴θ=
故选D
| a |
| b |
| a |
| b |
| a |
| b |
∴（
| a |
| b |
| a |
| b |
| a |
| b |
即
| a |
| b |
| 1 |
| 2 |
| a |
| 1 |
| 2 |
| b |
∴cosθ=
| ||||
|
|
| 1 |
| 2 |
∴θ=
| 2π |
| 3 |
故选D
点评：本题主要考查了平面向量的数量积的性质：若
⊥
?
•
=0=0的应用，即若知道向量垂直，则可得向量的数量积为0．
| a |
| b |
| a |
| b |
练习册系列答案
相关题目
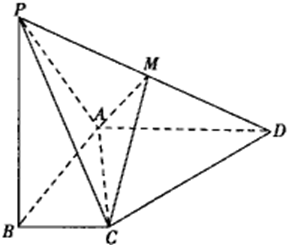（2012•许昌一模）已知四棱锥P-ABCD中，底面ABCD是直角梯形，∠BAD=∠CBA=90°，面 PAB⊥面ABCD，PA=PB=AB=AD=2，BC=1．