题目内容
(2012•许昌一模)已知函数f(x)=lnx-x+ax2.
(I)试确定实数a的取值范围,使得函数f(x)在定义域内是单调函数;
(II)证明:
(
-ln
)>
.
(I)试确定实数a的取值范围,使得函数f(x)在定义域内是单调函数;
(II)证明:
| n |
 |
| k=2 |
| 1 |
| k |
| 1 |
| k |
| n-1 |
| 2(n+1) |
分析:(Ⅰ)使得函数f(x)在定义域内是单调函数,则有f′(x)≥0或f′(x)≤0在定义域内恒成立,由此可求a的范围;
(Ⅱ)利用(Ⅰ)问结论,令a=1,此时f(x)<0对x∈(0,1)恒成立,由此构造不等式,再令x=
,对
(
-ln
)进行放缩变形即可.
(Ⅱ)利用(Ⅰ)问结论,令a=1,此时f(x)<0对x∈(0,1)恒成立,由此构造不等式,再令x=
| 1 |
| k |
| n |
 |
| k=2 |
| 1 |
| k |
| 1 |
| k |
解答:(Ⅰ)解:定义域为(0,+∞).f′(x)=
-1+2ax=
.
令g(x)=2ax2-x+1,
∵g(0)=1,∴g(x)≥0对x∈(0,+∞)恒成立.即a≥
对x∈∈(0,+∞)恒成立.
令h(x)=
=-
(
)2+
(
)=-
(
-
)2+
.
∴a≥
,此时f(x)在(0,+∞)上为单调递增函数.
(Ⅱ)证明:取a=1,由(Ⅰ)知此时f(x)在(0,1)上为单调递增函数.
∵f(1)=0,∴f(x)<0对x∈(0,1)恒成立,即x-lnx>x2.
取x=
,∵
∈(0,1),∴
-ln
>(
)2.
∴
(
-ln
)>
(
)2>
=
(
-
)=
-
=
.
| 1 |
| x |
| 2ax2-x+1 |
| x |
令g(x)=2ax2-x+1,
∵g(0)=1,∴g(x)≥0对x∈(0,+∞)恒成立.即a≥
| x-1 |
| 2x2 |
令h(x)=
| x-1 |
| 2x2 |
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 8 |
∴a≥
| 1 |
| 8 |
(Ⅱ)证明:取a=1,由(Ⅰ)知此时f(x)在(0,1)上为单调递增函数.
∵f(1)=0,∴f(x)<0对x∈(0,1)恒成立,即x-lnx>x2.
取x=
| 1 |
| k |
| 1 |
| k |
| 1 |
| k |
| 1 |
| k |
| 1 |
| k |
∴
| n |
 |
| k=2 |
| 1 |
| k |
| 1 |
| k |
| n |
 |
| k=2 |
| 1 |
| k |
| n |
 |
| k=2 |
| 1 |
| k(k+1) |
| n |
 |
| k=2 |
| 1 |
| k |
| 1 |
| k+1 |
| 1 |
| 2 |
| 1 |
| n+1 |
| n-1 |
| 2(n+1) |
点评:本题考查导数的应用,一是研究函数单调性,二是证明不等式,证明不等式的关键是利用条件恰当构造不等式,对能力要求较高.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
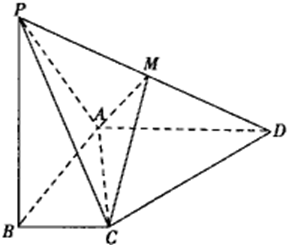 (2012•许昌一模)已知四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=∠CBA=90°,面 PAB⊥面ABCD,PA=PB=AB=AD=2,BC=1.
(2012•许昌一模)已知四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=∠CBA=90°,面 PAB⊥面ABCD,PA=PB=AB=AD=2,BC=1.