题目内容
已知各项均为正数的等比数列{an)的公比q=2,若存在两项am,an使得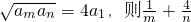 的最小值为
的最小值为
- A.

- B.

- C.

- D.不存在
B
分析:利用等比数列的性质可求得m+n=6(m∈N*,n∈N*),再利用基本不等式即可求得 +
+ 的最小值.
的最小值.
解答:∵各项均为正数的等比数列{an}的公比q=2,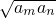 =4a1,
=4a1,
∴am=a1•qm-1=2m-1•a1,
同理an=2n-1•a1
∴am•an=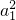 •2m+n-2=16
•2m+n-2=16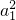 ,
,
∴2m+n-2=16=24,
∴m+n=6(m∈N*,n∈N*),
∴ +
+ =(
=( +
+ )×
)× (m+n)
(m+n)
= (1+4+
(1+4+ +
+ )
)
≥ (5+2
(5+2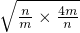 )
)
= ×9
×9
= (当且仅当m=2,n=4时取“=”).
(当且仅当m=2,n=4时取“=”).
故选B.
点评:本题考查等比数列的性质,考查基本不等式,求得m+n=6(m∈N*,n∈N*)是关键,也是难点,考查化归思想与方程思想,考查运算能力,属于中档题.
分析:利用等比数列的性质可求得m+n=6(m∈N*,n∈N*),再利用基本不等式即可求得
 +
+ 的最小值.
的最小值.解答:∵各项均为正数的等比数列{an}的公比q=2,
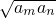 =4a1,
=4a1,∴am=a1•qm-1=2m-1•a1,
同理an=2n-1•a1
∴am•an=
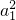 •2m+n-2=16
•2m+n-2=16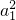 ,
,∴2m+n-2=16=24,
∴m+n=6(m∈N*,n∈N*),
∴
 +
+ =(
=( +
+ )×
)× (m+n)
(m+n)=
 (1+4+
(1+4+ +
+ )
)≥
 (5+2
(5+2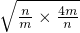 )
)=
 ×9
×9=
 (当且仅当m=2,n=4时取“=”).
(当且仅当m=2,n=4时取“=”).故选B.
点评:本题考查等比数列的性质,考查基本不等式,求得m+n=6(m∈N*,n∈N*)是关键,也是难点,考查化归思想与方程思想,考查运算能力,属于中档题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 ,
, 的等比中项。
的等比中项。 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。 中,
中, 与
与 的等比中项为
的等比中项为 ,则
,则 的最小值为( )
的最小值为( ) ,
, 的等比中项。
的等比中项。 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。 ,
, 的等比中项。
的等比中项。 是等差数列;
是等差数列; 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。 ,
, 的等比中项。
的等比中项。 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。